دوال الدرجة الثانية
حتى الآن رأينا كيف تبدو الأشكال البيانية لكل من متعددات الحدود من الدرجة صفر \((y=a)\) ومتعددات الحدود من الدرجة الأولى \((y=ax + b)\) على نظام الإحداثيات. الآن سنتعرف على شكل متعددات حدود الدرجة الثانية على نظام الإحداثيات.
سنبدأ بالدالة التالية:
$$y(x)=x^{2}$$
لكي نفهم كيف يبدو شكل هذا النوع من الدوال على نظام الإحداثيات سنقوم أولا بتكوين جدول القيّم التالي:
| \(f(x)\) | \(x\) |
| \(9\) | \(-3\) |
| \(4\) | \(-2\) |
| \(1\) | \(-1\) |
| \(0\) | \(0\) |
| \(1\) | \(1\) |
| \(4\) | \(2\) |
| \(9\) | \(3\) |
بعد ذلك نضع كل زوج من هذه القيّم \((x, y (x))\) كنقاط على نظام إحداثيات ثم نوصل هذه النقاط مع بعضها البعض:
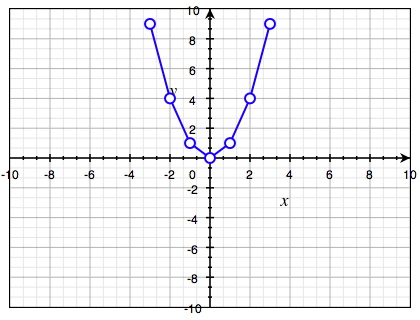
نلاحظ أن هذه العلاقة تُشكل منحنى متماثل في شكل حرف U يمر بنقطة الأصل. نلاحظ أن هذا المنحنى يحتوي على زوايا منفرجة جدا عند النقاط الموصلة، بمعنى أن لدينا منحنى زاوي. إذا قمنا بتحديد المزيد من النقاط سيكون لدينا منحنى غير زاوي. فإذا اخترنا استخدام عدد كبير من النقاط سيكون لدينا منحنى كما في الشكل التالي:
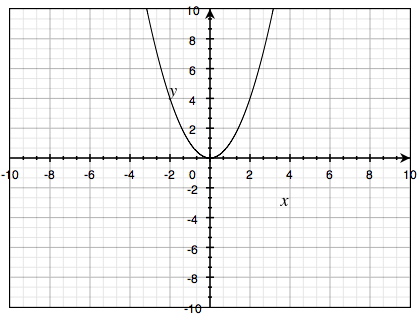
نلاحظ أن هذا المنحنى له نقطة صغرى عند نقطة الأصل (0, 0) وذلك لأن معامل \(x^ 2\) في هذه الدالة موجب (وهو واحد صحيح في هذه الحالة).
نواصل مع دالة أخرى:
$$y(x)=-x^{2}$$
هذه الدالة مشابهة للدالة السابقة ولكن إذا نظرنا إلى شكلها على نظام الإحداثيات سنلاحظ اختلاف واضح بينهما.
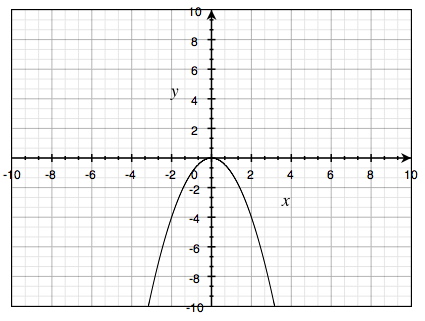
فعندما يكون معامل \(x^2\) في هذا النوع من الدوال عدد سالب (وهو \(-1\) في هذه الحالة) سيكون المنحنى عبارة عن صورة مقلوبه لمنحنى الدالة السابق وله نقطة عظمى عند نقطة الأصل (0, 0).
جميع دوال الدرجة الثانية لها شكل القطع المكافئ ولكن تختلف عن بعضها البعض في العرض والموقع على نظام الإحداثيات وذلك وفقا لقيّم المعاملات والثوابت.
أمثلة على دوال الدرجة الثانية
$$y(x)=3x^{2}+1$$
$$y(x)=2x^{2}+4x$$
$$y(x)=x^{2}+4x-8$$
$$y(x)=-x^{2}+x+6$$
سابقا تعلمنا أن معادلات الدرجة الثانية قد يكون لها جذرين حقيقيين، جذر حقيقي واحد أو قد لا يكون لها أي جذر حقيقي (ليس لها حل حقيقي). وهذا سيكون أكثر وضوحا عندما ندرس أشكال الدوال بيانياً على نظام الإحداثيات.
عندما يكون لدينا دالة عادية من الدرجة الثانية تحتوي على نقطتي إنعدام (نقاط الدالة الصفرية) فغالبا ما نرى نقاط إنعدام الدالة بشكل واضح، أي النقاط التي يتقاطع فيها المنحنى مع محور \(x\) (حيث أن \(y=0\)). هذه النقاط هي قيّم \(x\) التي نقوم بحسابها عندما نحل معادلة من معادلات الدرجة الثانية.
فيما يلي مثال على هذا النوع من معادلات الدرجة الثانية
$$x^{2}-6x+5=0$$
يمكننا حل هذا النوع من معادلات الدرجة الثانية باستخدام صيغة-pq:
$$p=-6$$
$$q=5$$
$$x=-\frac{(-6)}{2}\pm \sqrt{\left (\frac{-6}{2} \right )^{2}-5}$$
$$x=3\pm \sqrt{4}=3\pm 2$$
$$x_{1}=5$$
$$x_{2}=1$$
يمكن كتابة الدالة المقابلة على النحو التالي
$$y(x)=x^{2}-6x+5$$
وسيكون شكل هذه الدالة كما يلي:
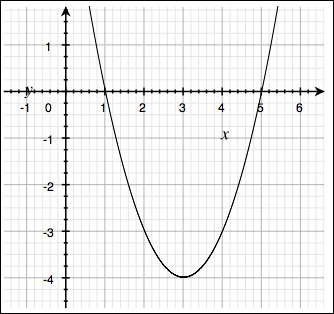
إذا نظرنا إلى شكل هذه الدالة في نظام الإحداثيات أعلاه سنلاحظ أن نقاط إنعدام الدالة (أي عند \(y (x)=0\)) ستكون على محور \(x\) فقط, بمعنى أن نقاط إنعدام الدالة عبارة عن قيّم \(x\) فقط وهي التي تُمثل حلول لهذه المعادلة.
يمكن أيضا أن يكون لدينا دالة تحتوي على نقطة إنعدام واحدة فقط
$$y(x)=x^{2}-2x+1$$
وسيكون شكل هذه الدالة كما يلي:
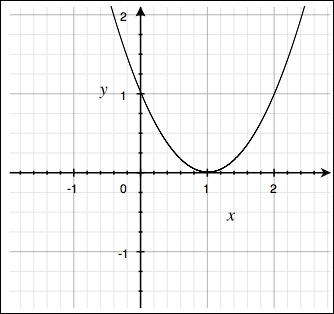
نلاحظ أن منحنى هذه الدالة يمس محور \(x\) عند نقطة واحدة وعند هذه النقطة لدينا أن \(y=0\) و \(x = 1\). يمكننا التحقق من ذلك بحل معادلة الدرجة الثانية المقابلة:
$$ x^{2}-2x+1 = 0$$
لنحل هذا المعادلة باستخدام صيغة-pq:
$$x=-\frac{(-2)}{2}\pm \sqrt{\left (\frac{(-2)}{2} \right )^{2}-1}$$
$$x=1\pm \sqrt{1-1}=1 \pm 0=1$$
بما أنه لدينا جذر واحد لهذه المعادلة وهو \(x = 1\), فهذا يعني صحة نتيجة دراستنا لشكل الدالة البياني أعلاه. نقطة أنعدام هذه الدالة الوحيدة هي عند \(x = 1\) (نقطة انعدام قيمة \(y\)).
في الختام سنرى الشكل البياني لمعادلة من معادلات الدرجة الثانية التي ليس لها جذور حقيقية
$$x^{2}-2x+2=0$$
إذا حاولنا حل هذه المعادلة بإستخدام صيغة-pq سنحصل على:
$$p=-2$$
$$q=2$$
$$x=-\frac{(-2)}{2}\pm \sqrt{\left (\frac{(-2)}{2} \right )^{2}-2}$$
$$x=1\pm \sqrt{1-2}=1\pm \sqrt{-1}$$
بما أننا تحصلنا على تعبير لقيمة \(x\) يحتوي على جذر لعدد سالب يمكننا أن نستخلص أن هذه المعادلة ليس لها حل حقيقي.
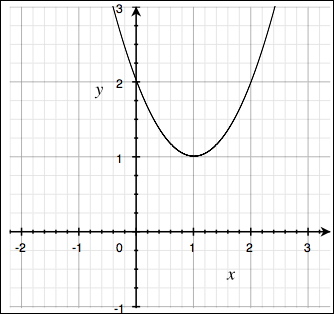
دالة الدرجة الثانية المقابلة هي كما يلي:
$$y(x)=x^{2}-2x+2 $$
في الشكل أدناه نلاحظ أن الرسم البياني لهذه الدالة مثير للإهتمام وذلك لأن الدالة ليس لها نقاط إنعدام (لا توجد أي قيمة لــ \(x\) يمكننا اختيارها عندما تكون \(y (x)=0\)) بمعنى أن منحنى الدالة لا يتقاطع مع محور \(x\) على الإطلاق, بينما يبقى دائما في مستوى أعلى من محور \(x\).
فيديوهات الدرس
مقدمة عن دوال الدرجة الثانية.
مفهوم قمة وقاع منحنى دوال الدرجة الثانية وخط التماثل.
نقاط إنعدام الدالة وتقاطعها مع محور y.
أكبر قيمة وأدنى قيمة لدوال الدرجة الثانية.
قاعدة تذكيرية صغير لشل دوال الدرجة الثانية.
