العدد e

في الكورس رياضيات 2 تعلمنا كيف نتعامل مع الدوال الأُسية.

الصورة العامة للدوال الأُسية هي:

$$f(x)=c\cdot a^{x}$$

حيث أن c و a ثوابت

فيما يلي مثال على دالة أسية

$$f(x)=2^{x}$$

في القسم السابق استعرضنا قواعد التفاضل لمجموعة من دوال متعددات الحدود الأكثر شيوعاً. في هذا القسم سندرس إشتقاق دالة خاصة من الدوال الأُسية وهي الدالة التي تحتوي على العدد \(e\).

هل هنالك دالة تساوي مُشتقتها؟

بمعنى أن هل هنالك دالة \(f(x)\) تساوي مُشتقتها \(f' (x)\), بعبارة أخرى هل \(f'(x) = f(x)\)؟

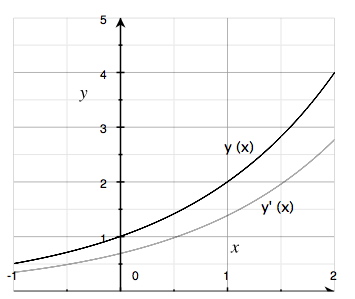
في الشكل التالي تم رسم كل من منحنى الدالة \(f(x) =2^x\) ومنحنى مشتقتها \(f'(x)\). منحنى المُشتقة يقع أسفل منحنى الدالة, لاحظ تشابه منحنى الدالة مع منحنى المشتقة.

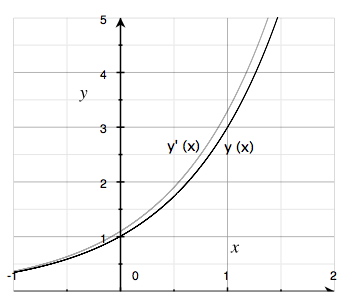
في الشكل التالي تم رسم منحنى الدالة \(y = 3^x\) ومنحنى مشتقتها. في هذه المرة يقع منحنى المُشتقة أعلى (فوق) منحنى الدالة، أيضا نلاحظ تشابه المنحنيين.

يمكننا إعادة صياغة السؤال أعلاه كما يلي: هل هنالك دالة أُسية ينطبق منحناها مع منحنى مُشتقتها تماماً؟

الإجابة هي نعم والدالة التي لها هذه الخاصية هي $$f(x)=e^{x} $$

العدد \(e\) الوارد في الدالة أعلاه هو عبارة عن عدد غير نسبي ويساوي 2,72 تقريبا. في القسم القادم سنناقش كيف وصلنا الى ذلك.

فيما يلي نلخص قاعدة تفاضل هذه الدالة

\(f(x)\)	\(f'(x)\)
\(e^x\)	\(e^x\)