قابلية التفاضل والقيمة المطلقة

في هذا القسم سنشرح مفهوم قابلية تفاضل (إشتقاق) الدوال كما سنشرح الحالات التي تكون فيها الدوال غير قابله للتفاضل عند نقاط معينة.

تكون الدالة قابله للتفاضل عند نقط معينة إذا كان بالإمكان رسم مماس واحد فقط عند هذه النقطة ويجب أيضا أن تكون الدالة مُعرّفة ومُستمرة عند هذه النقطة. من ناحية أخرى هنالك دوال مُعرّفه ومُستمرة عند نقطة معينة ولكنها غير قابله للتفاضل عند تلك النقطة.

التعريف عند نقطة

إذا كان هنالك دالة مُعرّفة عند نقطة ما فهذا يعني أن قيمة \(x\) من احداثيات هذه النقطة تدخل في مجال الدالة. لتوضيح هذا المفهوم بصورة أفضل سندرس قابلية التفاضل للدالتين التاليتين.

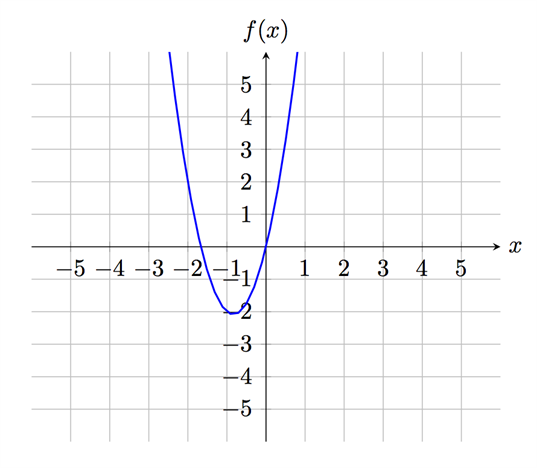
الدالة الأولى: \(f(x)=3x^2+5x\)

هذه الدالة مُعرّفة لكل قيّم \(x\) وهذا يعني أن هذه الدالة قابلة للتفاضل عند جميع قيّم \(x\). وذلك لأنه يمكننا الحصول على قيمة لــ \(y\) بتعويض أي قيمة من قيّم \(x\), بمعنى أخر كل قيّم \(x\) تدخل ضِمن مجال هذه الدالة.

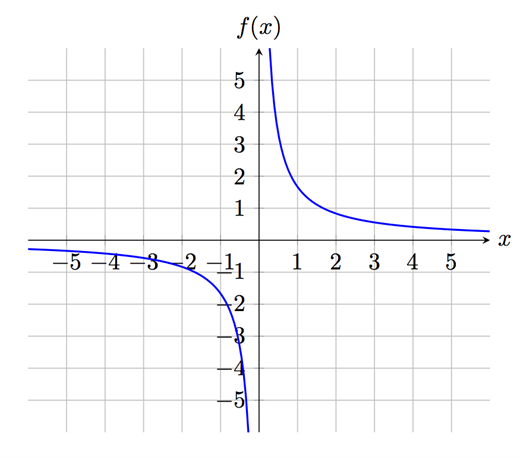
الدالة الثانية: \(f(x)=\frac{5}{3x}\)

يمكننا مباشرةً ملاحظة أن هذه الدالة ليست مُعرّفة عند النقطة \(x=0\) لأن هذه الدالة عبارة عن حاصل قسمة مقامها يتكون من عملية ضرب تحتوي على العامل \(x\). إذا عوضنا قيمة \(x=0\) سنحصل على \(\frac{5}{3\cdot 0}\), وهذه عبارة عن قيمة غير مُعرّفة. ما يعني أن هذه الدالة غير مُعرّفة عند النقطة \(x=0\).

الدوال المستمرة

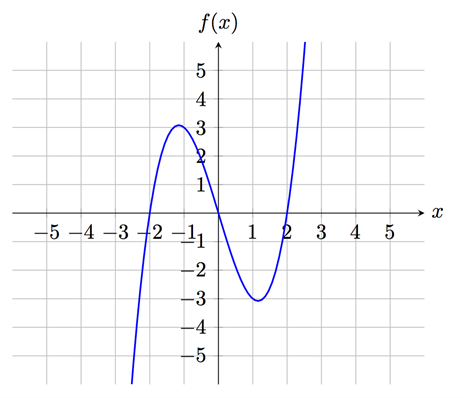
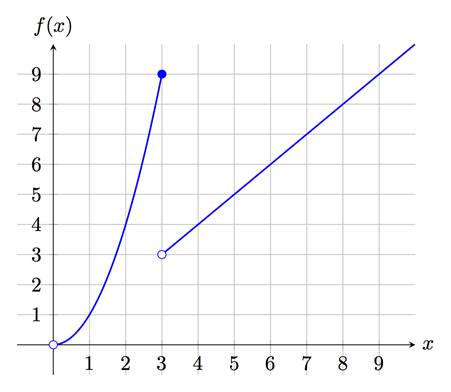
الدالة مستمرة يعني أن الدالة متصلة، أي غير متقطعة.. وبطريقة أخرى يمكن أن نقول أن الدالة مستمرة إذا استطعنا رسم الدالة بدون رفع القلم، فإذا كانت الدالة غير متصله فهذا يعني أن الدالة غير مُستمرة (متقطعة). فيما يلي سنرسم دالتين, الأولى مستمرة والثانية غير مستمرة.

القيمة المُطلقة

إذا كان لدينا عدد حقيقي موجب أو سالب فقد يكون من المفيد معرفة المسافة التي يبعدها هذا العدد من نقطة الأصل. لنرى بعض الأمثلة:

العدد	البُعد من نقطة الأصل
\(7,3\)	\(7,3\)
\(-2,6\)	\(2,6\)
\(0\)	\(0\)
\(-13\)	\(13\)

هناك مُصطلح لهذه المسافة المعينة التي يبُعدها أي عدد حقيقي من نقطة الأصل - يُسمى بالقيمة المطلقة للعدد.

القيمة المُطلقة لأي عدد a نشير إليها بــ \(|a|\). يمكن تعريف القيمة المطلقة للعدد a على النحو التالي:

$$\left | a \right |=a, om \: a\geq 0$$

$$\left | a \right |=-a, om \: a < 0 $$

عمليا هذا يعني أن القيمة المُطلقة \(|a|\) دائما موجبة سواءاً كان العدد a موجب أم سالب.

الدوال المُعرّفة ومُستمرة عند نقطة مُعينة ولكنها غير قابلة للتفاضل

كما ذكرنا في مقدمة هذا القسم هنالك دوال مُعرفة ومستمرة عند نقطة معينه ولكنها غير قابلة للتفاضل عند هذه النقطة. هذا يحدث عندما يكون لدينا على سبيل المثال دالة تحتوي على قيمة مطلقة. لننظر الى شكل الدالة \(f(x)=|x-2|\):

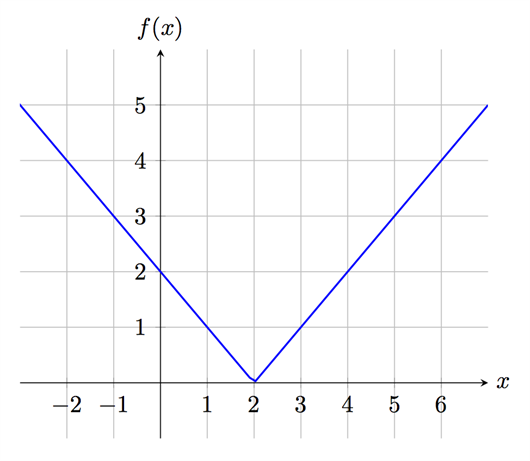
كما نلاحظ في الشكل أعلاه أن هذه الدالة لها زاوية عند النقطة \((2,0)\). هذه الدالة معرفة ومستمرة عند هذه النقطة ولكنها غير قابلة للتفاضل. غير قابلة للتفاضل لأنه يمكننا رسم مماسين عند هذه النقطة وذلك حسب الإتجاه الذي نبدأ منه لتقترب قيمة \(x\) من الــ \(2\). فإذا إقتربنا من النقطة \((2,0)\) قادمين من الجهة اليسرى فسيكون لدينا مماس ميله \(-1\), أما إذا إقتربنا منها قادمين من الجهة اليمنى فسيكون لدينا مماس ميله \(1\).

فيديو الدرس

كيفية حساب القيمة المطلقة للأعداد الحقيقية.