تعريف المُشتقة بإستخدام المسافة-h

في الأقسام السابقة قمنا بصياغة نسبة التغيُّر ورأينا كيف يمكن حساب قيمة نهاية الدالة. الآن سنقوم بصياغة تعبير عام يمكن استخدامه لحساب قيّم جميع النهايات. لنتخيل أن لدينا الدالة العامة \(y =f (x)\) ونختار نقطة عشوائية إحداثياتها \((x, f (x))\):

ثم نختار نقطة أخرى تبعُد مسافة h من النقطة الأولى \((x, f (x))\). ولتكن إحداثيات النقطة الثانية هي \(((x + h), f (x + h))\):

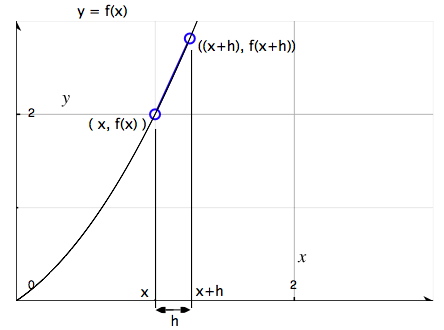
يمكن حساب قيمة-k للخط الواصل بين هاتين النقطتين كما يلي:

$$k=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}$$

فإذا إقتربت النقطة \(((x + h), f (x + h))\) من النقطة \((x, f (x))\) أكثر فأكثر فهذا يعني أن المسافة h تقترب من الصفر:

$$h\rightarrow 0$$

(هذا هو نفس المنطق الذي استخدمناه في قسم ميل المماس، حيث عرّفنا صيغة نسبة التغيُّر، ولكن في المرة السابقة إستخدمنا النقطة \((2, f (2))\) وجعلنا النقطة الأخرى \((x, f (x))\) تقترب من النقطة الأولى وذلك بإقتراب \(x\) من \(-2\).

قيمة النهاية لــ \((x, f (x))\) ستكون كما يلي:

$$k=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{(x+h)-x}=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$

هذا التعبير يُسمى بــ "تعريف المشتقة بإستخدام المسافة-h".

لنستخدم هذه الصيغة لحساب مشتقة الدالة \(f\) عند النقطة التي يكون فيها \(x =a\), أي لنحسب \(f '(a)\):

$$ f'(x) =\lim_ {h\rightarrow 0} \frac{f (x + h) -f (x)}{h} $$

$$f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}$$

فيديوهات الدرس

تعريف المُشتقة بإستخدام المسافة-h.

الإشتقاق باستخدام تعريف المُشتقة بإستخدام المسافة-h.