قاعدة مساحة المُثلث

في الكورس رياضيات 1 تعلمنا العلاقة بين مساحة المُثلث (A) وقاعدته (b) وارتفاعه (h):

$$Area=\frac{b\cdot h}{2}$$

يمكننا حساب مساحة المُثلث بإستخدام هذه العلاقة إذا علمنا كل من قاعدة وإرتفاع المُثلث. ولكن هناك طريقة أخرى جيدة لحساب مساحة المُثلث حتى إذا لم يكن لدينا هذه المعلومات. وفي هذه الحالة يمكننا حساب مساحة المثُلث بإستخدام قاعدة المساحة التالية:

$$Area=\frac{b\cdot c\cdot sin \: \alpha}{2}$$

حيث \(b\) و \(c\) هما ضلعين من أضلاع المثلث و \(\alpha\) هي الزاوية المحصورة بينهما كما في المثلث أدناه:

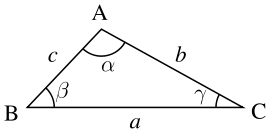
بنفس الطريقة يمكننا حساب مساحة المثلث بإستخدام أي ضلعين آخرين والزاوية المحصورة بينهما إذا علمنا طول كل منهما وقيمة الزاوية المحصورة بينهما:

$$Area=\frac{a\cdot c\cdot sin \: \beta}{2}$$

$$Area=\frac{a\cdot b\cdot sin \: \gamma}{2}$$

---

لنأخذ مثال على كيفية تطبيق قاعدة مساحة المُثلث

احسب مساحة المثلث الذي طول أحد أضلاعه 3 سم وطول الضلع الآخر 4 سم والزاوية المحصورة بينهما \(50°\).

لتكن الأضلاع المعلومة هي \(a\) (3 سم) و \(b\) (4 سم), والزاوية المحصورة بينهما \(\gamma = 50°\), يمكننا استخدام قاعدة المساحة كما يلي:

$$Area=\frac{3\cdot 4\cdot sin \: 50^\circ}{2}\approx 4,6 \: cm^2$$

---

فيديوهات الدرس

في هذا الفيديو سنشرح قاعدة مساحة المُثلث.

كيفية إستخدام الآلة الحاسبة

في هذا الفيديو تم إستخدام الآلة الحاسبة البيانية Casio FX-CG20.
شاهد نفس التمرين على الآلة الحاسبة البيانية Casio FX-9750GII.

الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريباً.