المساحة بين منحنيين
في القسم السابق درسنا مفهوم التكامل وكيفية حساب المساحة بين منحنى الدالة ومحور \(x\) من خلال حساب التكامل.
فإذا أردنا حساب المساحة بين منحنيين، كيف يمكن حسابها؟
نأخذ مثال
فيما يلي لدينا نظام إحداثيات مرسوم عليه مُنحنيين. المنحنى الأعلى هو منحنى الدالة \(f (x) =2x + 4\) والمنحنى الأسفل هو منحنى الدالة \(g (x) =-3x + 2\).
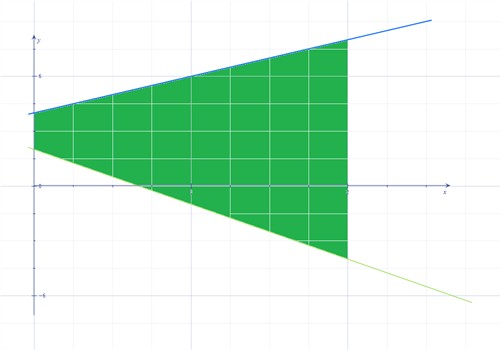
في هذه الحالة يتم حساب مساحة المنطقة على النحو التالي:
$$A=\int_{a}^{b}(f(x)-g(x))dx$$
عادة ما تكون \(f (x)\) هي المنحنى الواقع في أعلى المساحة و\(g (x)\) هي المنحنى الواقع في أسفل المساحة. وفي هذه الحالة يتم حساب المساحة بين المنحنيين في الفترة ما بين \(x =0\) إلى \(x =2\) كما يلي:
$$A=\int_{0}^{2}((2x+4)-(-3x+2))dx =$$
$$= \int_{0}^{2}(5x+2)dx$$
بعد ذلك سنركز على الطرف الأيمن للتكامل: سنوجد الدالة الأولية ونستخدم حدود التكامل لحساب المساحة.
إذا استخدمنا الرمز \(h (x)\) كرمز للفرق بين الدالتين
$$h(x)=f(x)-g(x)=5x+2$$
فسيكون لدينا الدالة الأولية \(H (x)\) كما يلي:
$$H(x)=\frac{5x^2}{2}+2x+C$$
بإستخدام هذه المعلومات يمكننا حساب المساحة كما يلي:
$$A=\int_{0}^{2}h(x)\:dx = \left [ H(x) \right ]_0^2$$
$$A=\int_{0}^{2}(5x+2)\:dx = \left [ \frac{5x^{2}}{2} +2x \right ]_0^2=$$
$$=\frac{5\cdot 2^{2}}{2}+2\cdot 2=10+4=14 \: a.e.$$
إذن مساحة المنطقة المحدودة بالمنحنيين \(f (x) =2x + 4\) و \(g (x) =-3x + 2\) والخطين الرأسيين \(x =0\) و \(x =2\) هي 14 وحدة مساحية.
فيديو الدرس
في هذا الفيديو سنشرح طريقة حساب المساحة بين مُنحنيين.
إستخدام الآلة الحاسبة البيانية
هُنا تم إستخدام الآلة الحاسبة البيانية Casio FX-CG20.
شاهد نفس التمرين على الآلة الحاسبة البيانية Casio FX-9750GII.
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريباً.
