رسم المُنحنيات

في هذا القسم سنرى كيف يمكننا رسم الدوال بيانيا وذلك بإستخدام ما تعلمناه عن المشتقات في الأقسام السابقة.

رسم المُنحنيات بيانيا

الآن سندرس بعض خصائص الدالة التالية

$$f(x)=x^{2}-x-2$$

(a) ما هي الفترة التي تتزايد فيها هذه الدالة؟

مشتقة الدوال المتزايدة عادة ما تكون أكبر من الصفر عند نقاط فترة التزايد. يمكننا استخدام طريقة دراسة إشارات الحدود إذا بدأنا بإيجاد قيم \(x\) عند النقاط التي تكون فيها المشتقة صفر.

نشتق الدالة ونساوي المشتقة بالصفر وبحل هذه المعادلة سنحصل على قيّم \(x\) المطلوبة:

$$f'(x)=2x-1$$

$$0=2x-1$$

$$x=0,5$$

في هذه الحالة لدينا قيمة واحد فقط لــ \(x\) \((x =0.5)\), ما يعني أن الدالة لها نقطة واحدة فقط حيث سيكون المماس عندها أفقي (لأن المشتقة تساوي صفر).

حتى الآن لا نعلم موقع هذه النقطة بالنسبة لمحور \(y\) ولم نتعرّف على نوعها، هل هي نقطة صغرى أم عظمى أم سرجية.

ومع ذلك يمكننا أن نبدأ برسم الدالة بناءا على ما تحصلنا عليه عن هذه النقطة - نعلم أن المُشتقة في هذه النقطة تساوي صفر (المماس موازي لمحور \(x\)) ونعلم أن قيمة \(x\) عند هذه النقطة تساوي \(0, 5\):

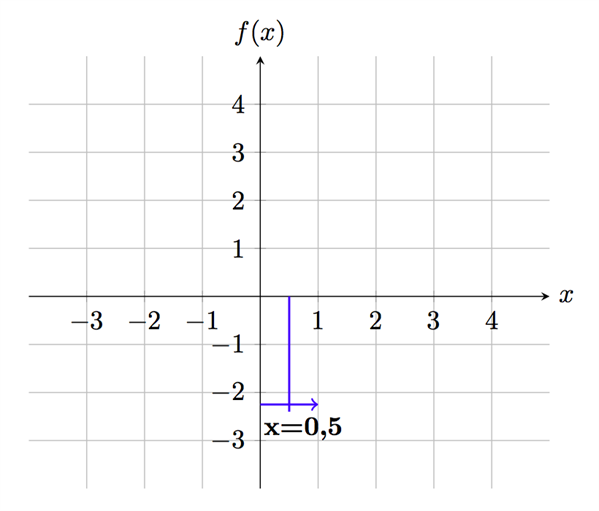
لنحاول الآن أخذ قيمة أخرى لـ \(x\) أكبر من \(0,5\) ونعوضها في تعبير المشتقة لنرى شكل الميل يمين هذه النقطة. بما أنه لدينا نقطة إنعدام واحدة فقط فهذا يعني أنه سيكون لدينا ميل واحد فقط على كل جانب (إما متزايد أو متناقص)، وإلا لوجدنا نقاط أكثر عندما بحثنا أصفار المشتقة سابقا:

$$f'(1)=2\cdot 1-1=1$$

عندما تكون \(x =1\) فإن المشتقة موجبة. بمعنى أن المنحنى يمين \(x =0,5\) سيكون متزايداً ويمكننا رسم هذا التزايد كما يلي:

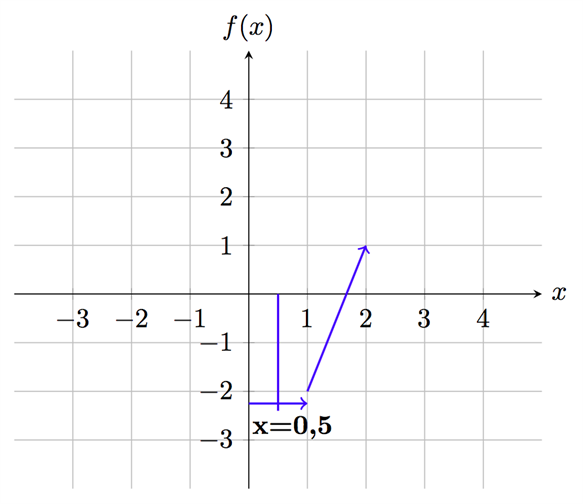
سنقوم بنفس الخطوات مع قيمة من قيّم \(x\) الأقل من \(0,5\) ونرى شكل المُشتقة يسار هذه النقطة:

$$f'(0)=2\cdot 0-1=-1$$

أي أن المُشتقة سالبة عند \(x =0\) وهذا يعني أن المنحنى يسار \(x =0,5\) سيكون متناقصاً. وبإضافة هذا التناقص إلى الشكل أعلاه يمكننا أن نتخيل شكل المنحنى كما في الشكل التالي:

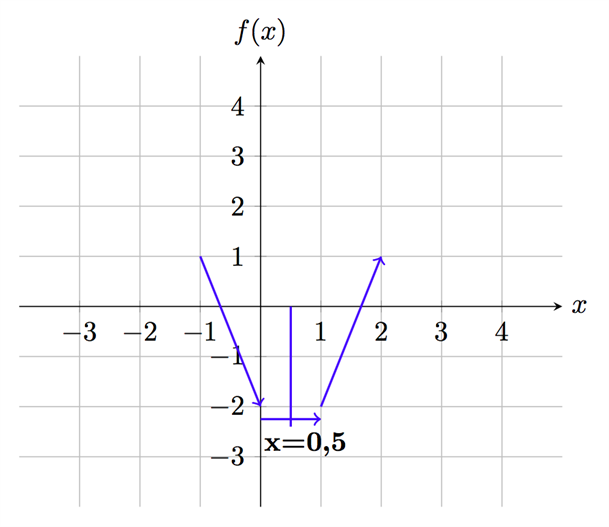
الآن لدينا معلومات كافية ويمكننا أن نقول أن المنحنى يشبه الفم الضاحك وله قيمة صُغرى عند \(x =0,5\). وللإجابة على السؤال الأساسي يمكننا أن نقول أن الدالة متزايدة لقيّم \(x\) في الفترة

$$x> 0,5$$

وهي عبارة عن جميع النقاط الواقعة يمين النقطة الصُغرى على المنحنى.

(b) أوجد نقاط المنحنى الصفرية وموقع النقطة الصُغرى.

قد يكون من السهل أن نخلط بين عملية إيجاد نقاط إنعدام الدالة (الأصفار) وعملية إيجاد قيّم \(x\) الممكنة للنقاط القصُوى (حيث توجد نقاط إنعدام المُشتقة). عند النقاط القصُوى الممكنة ستكون المُشتقة صفر ( \(f '(x) =0\))؛ بينما في حالة نقاط إنعدام الدالة ستكون قيمة الدالة نفسها صفر (\(f (x) =0\) وفي هذه الحالة سنكون عند نقطة ما على محور \(x\)).

إذا بدأنا بوضع \(f (x) =0\) سنحصل على أصفار المنحنى (نقاط إنعدام الدالة), أي إيجاد قيّم \(x\) عند نقاط تقاطع المنحنى مع محور \(x\) كما يلي:

$$f(x)=x^{2}-x-2$$

$$x^{2}-x-2=0$$

$$x=-\frac{(-1)}{2} \pm\sqrt{\left ( \frac{(-1)}{2} \right )^{2}-(-2)}=$$

$$=\frac{1}{2} \pm\sqrt{\frac{9}{4}}=\frac{1}{2} \pm\frac{3}{2}$$

$$\begin{align} x_{1} & =2 \\ x_{2} & =-1 \end{align}$$

وهذه هي نقاط إنعدام الدالة (الأصفار) المطلوبة:

في السؤال (a) أعلاه تم حساب قيمة \(x\) لإحداثيات النقطة الصُغرى وكل ما نحتاج إليه الآن هو الإحداثي \(y\). إذا كان لدينا قيمة \(x\) كيف يمكننا إيجاد قيمة \(y\)؟ حسنا, عوض قيمة \(x\) في الدالة \(f (x)\):

$$f(0,5)=0,5^{2}-0,5-2=-2,25$$

بالتالي إحداثيات النقطة الصُغرى هي \((0.5, -2.25)\).

بناءاً على المعلومات التي تحصلنا عليها من (a) و (b) يمكننا أن نلخص هذا التمرين من خلال رسم مُنحنى الدالة \(f(x)=x^{2}-x-2\) كما يلي:

---

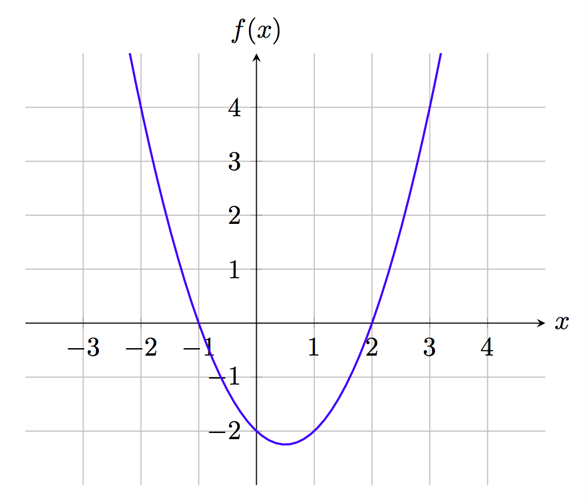
أوجد قيمة الدالة الكُبرى في الفترة المُحددة:

$$f(x)=x^{4}-2x^{2}$$

$$-1< x\leq 2$$

نبدأ بتحديد قيّم \(x\) للنقاط القصُوى وذلك بنفس الطريقة أعلاه، أي باشتقاق الدالة ومساواة المُشتقة بالصفر ومن ثم حَل المعادلة الناتجة:

$$f{}'(x)=4x^{3}-4x$$

$$0=4x\cdot (x^{2}-1)$$

$$x_{1}=0$$

$$x^{2}-1=0 \Rightarrow$$

$$\begin{align} x_{2} & =1 \\ x_{3} & =-1\end{align}$$

لاحظ أن \(x_3 = -1\) تقع خارج الفترة المُحددة ولهذا فإن قيمة الدالة عند هذه النقطة القُصوى يمكن تجاهلها لأنها خارج الفترة المُراد دراستها.

خلاف ذلك لدينا نقطتين قُصوتين ومن المُرشح أن يكونا عبارة عن قيّم الدالة الكُبرى في هذه الفترة. لدينا قيمة قُصوى تقع في مكان ما حيث \(x = 0\) وقيمة قُصوى أخرى تقع في مكان ما حيث \(x =1\).

لنحسب قيّم الدالة (قيّم \(y\)) عند النقاط الثلاث أي عند النقاط التي تكون عندها المشتقة صفر.

$$f(-1)=(-1)^{4}-2\cdot (-1)^{2}=1-2=-1\Rightarrow (-1,-1)$$

$$f(0)=0^{4}-2\cdot 0^{2}=0\Rightarrow (0,0)$$

$$f(1)=1^{4}-2\cdot 1^{2}=-1\Rightarrow (1,-1)$$

نحدد هذه النقاط الثلاث في الشكل التالي لكي نحصل على صورة أفضل لشكل المنحنى:

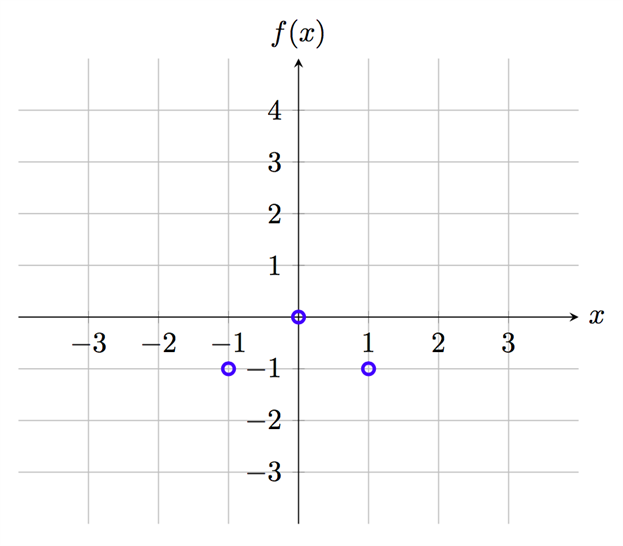
من هنا نواصل في دراسة الإشارات. الغرض من دراسة الإشارات هو أن نتعرّف على نوع هذه النقاط، كُبرى أم صُغرى أم سرجية. وللتأكيد سنقوم بدراسة المنحنى كاملا بما في ذلك الجزء الواقع خارج الفترة المُحددة.

بالتالي سنقوم بتعويض القيّم التالية في مشتقة الدالة:

1- قيمة من قيّم \(x\) الأقل من \(-1\)

$$\begin{align} f'(-2) = 4\cdot (-2)^{3}-4\cdot (-2) = \hspace{1.1cm}&\\ = 4\cdot (-8)+8=-24\Rightarrow - \end{align}$$

2- قيمة من قيّم \(x\) الأكبر من \(-1\) وأقل من الصفر

$$\begin{align}f'(-0,5)=4\cdot (-0,5)^{3}-4\cdot (-0,5) = \hspace{9mm}&\\ =4\cdot (-0,125)+2=1,5\Rightarrow + \end{align}$$

3- قيمة من قيّم \(x\) الأكبر من الصفر وأقل من الواحد

$$\begin{align}f'(0,5)=4\cdot 0,5^{3}-4\cdot 0,5 = \hspace{2.8cm}&\\ =4\cdot 0,125-2=-1,5\Rightarrow -\end{align}$$

4- وأخيرا قيمة من قيّم \(x\) الأكبر من الواحد

$$\begin{align}f'(2)=4\cdot 2^{3}-4\cdot 2 = \hspace{1.8cm}&\\ =4\cdot 8-8=24\Rightarrow + \end{align}$$

لنضع هذه النتائج في جدول الإشارات التالي:

\(2\)	\(1\)	\(0.5\)	\(0\)	\(-0.5\)	\(-1\)	\(-2\)	\(x\)
\(+\)	\(0\)	\(-\)	\(0\)	\(+\)	\(0\)	\(-\)	\({f}'(x)\)

الآن يمكننا إكمال الشكل أعلاه بإستخدام معلومات جدول الإشارات. الآن نعلم كيفية ميل المنحنى بين النقاط التي تكون فيها المُشتقة صفر. بالإضافة إلى ذلك نعلم أيضا كيفية ميل المنحنى يسار النقطة القُصوى الواقعة في أقصى اليسار \((-1,-1)\) وكيفية ميل المنحنى يمين النقطة القُصوى الواقعة في أقصى اليمين \((1,-1)\).

لذلك فإن المنحنى سيكون مشابه للشكل التالي:

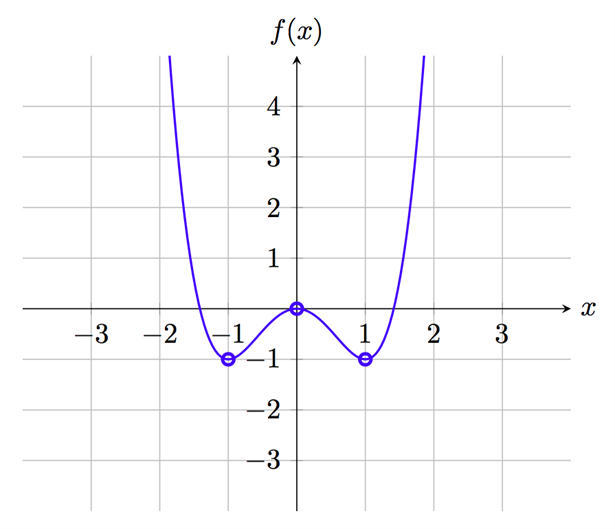
في مثل هذه الحالات علينا أن نكون حريصين ولا نتسرع ونستنتج أن قيمة الدالة الكُبرى هي \(f (0)\) بسبب أن لدينا نقطة عظمى. المطلوب هو إيجاد قيّم الدالة الكُبرى في الفترة التالية

$$-1< x\leq 2$$

وبما أن المنحنى يمين النقطة القُصوى \((1, -1)\) متزايد يجب علينا أن نتحقق من مقدار قيمة الدالة الكُبرى داخل الفترة التالية.

$$1< x\leq 2$$

من كيفية ميل المنحنى داخل هذه الفترة ستكون قيمة الدالة الكُبرى عند نقطة على المنحنى حيث \(x=2\). لذا سنحسب قيمة \(f (2)\) ونتأكد مما إذا كانت أكبر من \(f (0)\):

$$f(2)=2^{4}-2\cdot 2^{2}=16-8=8$$

بالتالي فإن أكبر قيمة للدالة في الفترة المُحددة هي: \(y =8\) (النقطة التي تكون فيها \(x = 2\)).

فيديو الدرس

شرح كيفية رسم المُنحنيات بإستخدام المُشتقة.