المُشتقات
في القسم السابق توصلنا الى أن المماس هو الخط الذي يلمس المنحنى في نقطة واحدة وله نفس ميل المنحنى عند هذه النقطة. فإذا كان لدينا قاطع يقطع منحنى عند نقطتين وسمحنا لتلك النقطتين بالاقتراب من بعضهما البعض بشكل كبير فسوف يقترب ميل القاطع من ميل المماس. عندما تقترب هاتين النقطين من بعضهما أكثر فأكثر وتقترب المسافة بينهما من الصفر أكثر فأكثر عندها سيصبح القاطع مماس. تُسمى نهاية نسبة التغير (القاطع / ميل المماس) والتي يمكننا حسابها بمشتقة الدالة عند تلك النقطة.
سابقا في هذا الكورس ناقشنا موضوع نهاية الدالة وذلك من خلال إيجاد نهاية قيمة الدالة في حالة إقتراب المتغير المستقل من قيمة معينة. في هذه المرة سنستخدم عملية حساب النهاية لإيجاد ميل المماس عند نقطة ما.
يمكن التعبير عن قيمة ميل المنحنى عند النقطة (b) الواقعة عند \((2, 2)\) بالنهاية التالية
$$k= \lim_{x \to 2 } \frac{f(x)-f(2)}{x-2}$$
lim تُشير إلى الكلمة اللاتينية "limes" والتي تعني "نهاية". بالتالي يمكننا أن نقول أن هذا التعبير مرتبط بقيمة \(k\) لمنحنى الشكل الأخير من القسم السابق (ميل المماس)، بينما التعبير
$$k= \frac{f(x)-f(2)}{x-2}$$
مرتبط بميل القاطع:
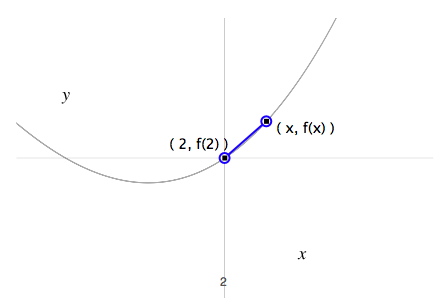
هناك طريقة أبسط لوصف قيمة النهاية عند النقطة (b).
$$k= \lim_{x \to 2 } \frac{f(x)-f(2)}{x-2}=f'(2)$$
\(f '(2)\) هي المُشتقة الأولى للدالة عندما تكون \(x =2\).
لنأخذ الآن مثال نحسب فيه المُشتقة الأولى لدالة معلومة عند نقطة معينة
فيما يلي لدينا الدالة ورسمها البياني.
$$f(x)=x^{2}+2x$$
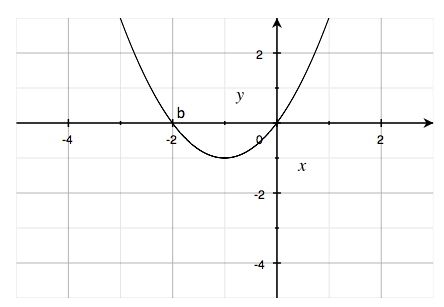
الآن سنحسب المُشتقة عند النقطة (b) (النقطة \(x =-2\) على المنحنى)
صيغة حساب قيمة هذه النهاية هي:
$$ k=f'(-2)= \lim_{x \to -2 } \frac{f(x)-f(-2)}{x-(-2)}$$
لا يمكننا تعويض \(x =-2\) في هذه الصيغة مباشرة لأن هذا يعني أننا نحاول حساب الميل بين (b) و (b) نفسها. بالطبع لا يمكننا استخدام نفس النقطة وتعويضها في الصيغة لمعرفة قيمة \(k\). فإذا حاولنا ذلك فسيصبح المقام صفرا وسيكون ناتج القسمة غير مُعرّف.
لحساب هذا النوع من النهايات يجب تحليل التعبير إلى عوامل ثم اختصاره. لنبدأ بحساب \(f (-2)\).
يتم حساب \(f (-2)\) كما يلي:
$$f(-2)=(-2)^{2}+2(-2)=4-4=0$$
أما \(f' (-2)\) ستكون:
$$f'(-2)=\lim_{x\rightarrow -2}\frac{f(x)}{x-(-2)}=\lim_{x\rightarrow -2}\frac{x^{2}+2x}{x+2}=$$
$$=\lim_{x\rightarrow -2}\frac{x\cdot (x+2)}{x+2}=\lim_{x\rightarrow -2}x=-2$$
إذن ميل المنحنى عند النقطة (b) \((x =-2)\), هو \(f '(-2) =- 2\)
ما هو الفرق بين \(f (x)\) و \(f '(x)\) عملياً؟ الشكل التالي يوضح كيفية ارتفاع شيء ما (مقذوف) الى الأعلى:
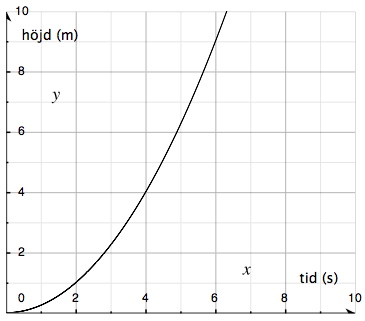
إذا درسنا النقطة \((2, 1)\):
\(f (2)\) هي ارتفاع هذا الشيء عندما كان الزمن ثانيتين \((x =2)\).
\(f '(2)\) هي مقدار تغيُّر الارتفاع عندما كان الزمن ثانيتين \((x =2)\) ويُمثل سرعة الشيء, أي مدى سرعة تغيُّر الارتفاع, عند النقطة الزمنية \(x =2\).
