المعادلات المثلثية
في القسم السابق تعرفنا على دائرة الوحدة ولاحظنا أنه يمكننا حساب إحداثيات أي نقطة على محيط دائرة الوحدة باستخدام دالتي جيب التمام والجيب إذا كانت الزاوية معروفة.
في هذا القسم سنتعلم بعض العلاقات الخاصة بدالتي الجيب وجيب التمام، وهذه العلاقات ستكون مفيدة جدا عند إجراء العمليات الحسابية.
دعونا نبدأ بمثال لمعادلة مثلثية
حِل المعادلة \(sin v =0.5\) باستخدام دائرة الوحدة.
كما تعلمنا في القسم السابق فإن حل المعادلة \(sin v =0.5\) يعني إيجاد مقدار الزاوية \(v\) التي تصنع نقطة على محيط الدائرة بحيث تكون قيمة الإحداثي \(y\) تساوي \(0,5\).
إذا نظرنا إلى الشكل أدناه سنلاحظ أن لدينا حلان لهذه المعادلة:
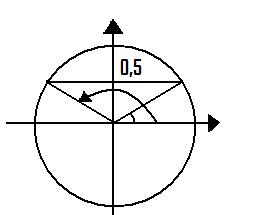
الحل الأساسي الأول يمكننا الحصول علية مباشرة باستخدام الآلة الحاسبة:
$$v_1=sin^{-1} \: 0,5=30^\circ$$
وكما ذكرنا أن لدينا حل آخر ويمكن ملاحظة ذلك في الشكل. يمكننا الحصول على زاوية هذا الحل بأن نبدأ من الصفر ونتحرك نصف دورة \((180°)\) ثم نرجع بمقدار زاوية تساوي زاوية الحل الأول \((30°)\).
الحل الأساسي الثاني هو:
$$v_2=180^\circ - v_1=180^\circ - 30^\circ=150^\circ$$
بالتالي الزاويتان \(30°\) و \(150°\) الإثنان يُمثلان حلّان لهذه المعادلة. ولكن يجب ألّا ننسى أنه إذا قمنا بزيادة الزاوية \(v\) بمقدار دورة كاملة \((360°)\) فإننا سنحصل على نفس قيمة جيب الزاوية \(v\).
إذن الحل الكامل لهذه المعادلة هو كما يلي:
$$v_1=30^\circ + n\cdot 360^\circ$$
$$v_2=150^\circ + n\cdot 360^\circ$$
حيث أن \(n\) عدد صحيح \(n =0, 1, 2, ...\)
بالتالي عندما يكون لدينا زوايا يمكن كتابتها بهذه الطريقة كالزاوية \(390°\) مثلاً \((30° + 1 \cdot 360°)\) ففي هذه الحالة يمكننا إستخدام هذا التعريف في حل المعادلات المُثلثية. هذا التعريف مفيد جداً ويمكن إستخدامه في وصف وتحليل عدد من الظواهر الدورية المختلفة، كمتوسط تغيّر درجات الحرارة خلال اليوم.
الطُرق التي إستخدمناها لإيجاد حَل المثال أعلاه يمكن ترجمتها الى صيّغ عامة كما يلي:
$$sin\:v=sin\:(180^\circ -v)$$
$$-cos\:v=cos\:(180^\circ -v)$$
$$-sin\:v=sin\:(360^\circ -v)$$
$$cos\:v=cos\:(360^\circ -v)$$
يمكن إثبات صحة كل من هذه العلاقات بتطبيقها على زوايا مختلفة في دائرة الوحدة.
فيديوهات الدرس
في هذا الفيديو سنشرح إثنين من المعادلات المُثلثية.
هنا سنشرح كيف يمكن تحقيق نفس الشروط المُثلثية بعدد من الزوايا المختلفة.
