دائرة الوحدة

في القسم السابق كررنا أساسيات المثلثات القائمة الزاوية والعلاقة بين الزوايا الحادة والأضلاع في المثلث القائم الزاوية.

لنقوم الآن بتعميم صيّغ الدوال المُثلثية التي درسناها في القسم السابق (ظل الزاوية، جيب الزاوية وجيب تمام الزاوية) ونعرفها للزوايا الأخرى. وهنا سنستخدم ما يُسمى بدائرة الوحدة، وهي إحدى الطُرق المفيدة لتحديد قيّم الدوال المثلثية لزوايا مختلفة. تتمركز دائرة الوحدة عند تقطة الأصل وطول نصف قطرها 1 وحدة طولية.

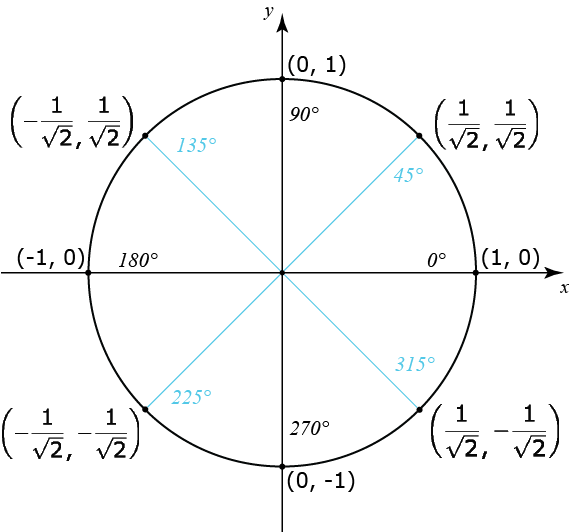
قيّم إحداثيات \(x\) و \(y\) لجميع النقاط الواقعة على محيط الدائرة يمكن قراءتها من محوري \(x\) و \(y\). إذا تخيلنا أن لدينا مثلث قائم الزاوية وله زاوية حادة \(t\) ضلعها المجاور عبارة عن جزء من محور \(x\) وضلعها المقابل هو الخط الموازي لمحور \(y\) والنازل من نقطة على محيط الدائرة عموديا على محور \(x\)، أنظر للشكل التالي:

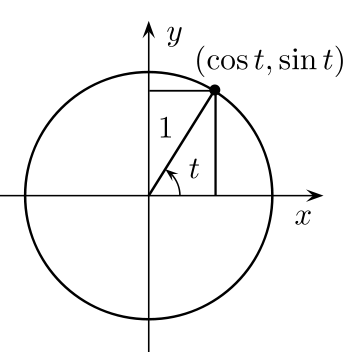
إذا استرجعنا تعريف الدوال المثلثية سيكون لدينا العلاقات التالية لجيب وجيب تمام الزاوية \(t\):

$$\sin t=\frac{y}{1}=y$$

$$\cos t=\frac{x}{1}=x$$

إذن للحصول على إحداثي \(x\) لنقطة من النقاط الواقعة على محيط الدائرة سنستخدم جيب تمام الزاوية؛ وللحصول على إحداثي \(y\) سنستخدم جيب الزاوية. بالتالي إحداثيات النقطة هي \((cos t, sin t)\), أي أن إحداثي \(x\) يُمثل الجتا و إحداثي \(y\) يُمثل الجيب.

فيديوهات الدرس

هنا سنشرح دائرة الوحدة وطريقة إستخدامها مع كل من الجيب (sinus), جيب التمام (cossinus) والظل (tangens).

شرح دائرة الوحدة وكيفية قراءة القيّم منها.