دوال متعددات الحدود
متعددة الحدود هي عبارة عن تعبير رياضي يتكون من متغيرات وثوابت مرتبطة ببعضها البعض بعمليات الجمع، الطرح والضرب. الحدود المتغيرة في متعددة الحدود عادة ما يكون لها أُسُس من الأعداد الصحيحة الموجبة فقط. وتعاملنا سابقا مع العديد من أشكال متعددات الحدود المختلفة حيث تعرفنا على هذا المفهوم في الكورسات السابقة. يتم تحديد درجة متعددة الحدود بأكبر أٌس فيها، يمكننا مشاهدة بعض الأمثلة في الجدول التالي:
| الإسم وفقا للدرجة | مثال |
| متعددة حدود من الدرجة صفر | \(1\) |
| متعددة حدود من الدرجة الأولي | \(2x+1\) |
| متعددة حدود من الدرجة الثانية | \(x^{2}+2x+1\) |
| متعددة حدود من الدرجة الثالثة | \(4x^{3}+3x^{2}+2x+1\) |
| متعددة حدود من الدرجة الرابعة | \(5x^{4}+4x^{3}+3x^{2}+2x+1\) |
أيضا تعلمنا طُرق حل معادلات متعددات الحدود ذات الدرجات الصغيرة كطريقة استخدام صيغة-pq في حل معادلات الدرجة الثانية. في القسم السابق تعلمنا أيضا دوال الدرجة الثانية (أي دوال متعددات الحدود ذات الدرجة الثانية)؛ ورأينا أيضا الشكل البياني لهذه الدوال وعلاقة الشكل البياني بحلول معادلة الدرجة الثانية المقابلة.
الرسم البياني لأي دالة من دوال الدرجة الأولى يكون دائما في شكل خط مستقيم، بينما يكون الرسم البياني لدوال الدرجة الثانية دائما في شكل قطع مكافئ.
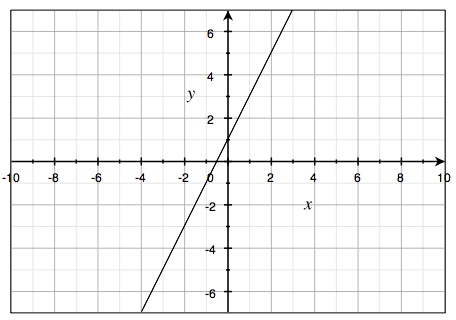
احدى دوال الدرجة الأولى التي رأيناها سابقا
$$y(x)=2x+1$$
الشكل البياني لهذه الدالة عبارة عن خط مستقيم:
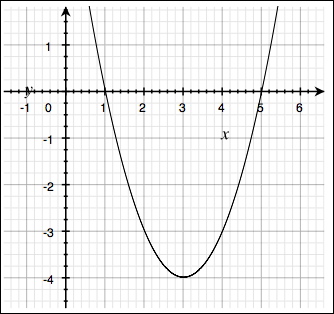
من العلاقات الأخرى المعروفة هي دوال الدرجة الثانية التي قابلتنا في القسم السابق
$$y(x)=x^{2}-6x+5$$
الشكل البياني لهذه الدالة هو على النحو التالي:
في هذا القسم سنرى خصائص الدوال متعددة الحدود ذات الدرجات الأعلى من الدرجة الثانية.
فيما يلي مثال على دالة من الدرجة الثالثة
$$ y(x)=x^{3}+3x^{2}+2x$$
تلعب درجة متعددة الحدود دورا كبيرا في شكل الرسم البياني للدالة، وهذا ما يمكن ملاحظته بمقارنة الرسوم البيانية لدالة من الدرجة الأولى ودالة من الدرجة الثانية. فيما يلي لدينا رسم بياني لدالة من دوال الدرجة الثالثة:
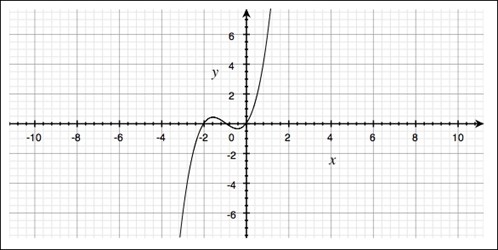
دوال الدرجة الأولى دائما تكون في شكل خط مستقيم ولها نقطة انعدام واحدة فقط وهي التي يتقاطع عندها الخط المستقيم مع محور \(x\).
كما ذكرنا سابقا يمكن أن تحتوي دوال الدرجة الثانية على نقطتي انعدام أو نقطة انعدام واحدة أو قد لا يكون لها نقاط انعدام. عدد نقاط إنعدام الدالة هي عدد المرات التي يتقاطع فيها المنحنى مع محور \(x\).
تحتوي دوال الدرجة الثالثة على ثلاثة نقاط إنعدام كما في حالة مثال الدالة أعلاه - من الرسم البياني يمكن ملاحظة أن المنحنى يتقاطع مع محور \(x\) عند \(x_1 =- 2\), \(x_2 =-1\) و \(x_3 =0\).
تحتوي متعددات الحدود من الدرجة n على n نقطة انعدام. في المقابل متعددة الحدود من الدرجة n سيكون لها n جذر.
بناء على شكل التعبير الرياضي لمتعددة الحدود يمكنك استخدام الطريقة البيانية لإيجاد نقاط انعدام دالة متعددة الحدود (كما فعلنا في هذا القسم) أو يمكنك استخدام الطريقة الجبرية لإيجاد جذور معادلة متعددة الحدود. وفي أغلب الأحيان قد يتم استخدام الطريقتين معا للحصول على نتائج دقيقة.
فيديو الدرس
حل معادلة من معادلات الدرجة الثالثة باستخدام الطريقتين البيانية والجبرية.
استخدام الآلة الحاسبة البيانية
هنا تم استخدام الآلة الحاسبة البيانية Casio FX-CG20.
شاهد نفس التمرين على الآلة الحاسبة البيانية Casio FX-9750GII.
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريباً.
