الدوال الأُسية
سابقا في هذا الكورس (رياضيات 2) درسنا الدوال الخطية و دوال الدرجة الثانية حيث كان لدينا المتغير المُستقل \(x\) عبارة عن أساس القوة.
الدالة التي يكون فيها المتغير المُستقل \(x\) هو عبارة عن القوة (الأُس) تُسمى بالدالة الأُسية.
يمكن كتابة الدوال الأُسية بصورة عامة كما يلي
$$y = C \cdot a^{x}$$
حيث أن \(C\) و \(a\) ثوابت \((a > 0)\), \(x\) هو المتغير المُستقل و \(y\) هو المتغير التابع. وكما نلاحظ أن الأُس هو المتغير المستقل \(x\) بينما أساس القوة هو الثابت \(a\).
قيمة الأساس a في الدالة الأسية
يختلف شكل الدالة الأسية اعتمادا على قيمة الأساس \(a\) أي إذا كانت قيمة الأساس \(a\) أكبر أم أصغر من 1 (قيمة الأساس \(a\) دائما أكبر من 0).
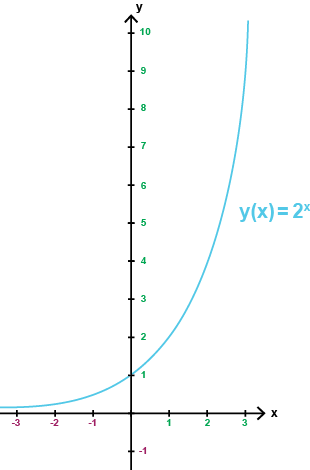
على نظام الإحداثيات التالي قمنا برسم مخطط بياني للدالة الأسية
$$y(x)=2^x$$
في هذه الدالة الأساس أكبر من 1 (a = 2)
في هذه الحالة تتزايد الدالة لجميع قيّم \(x\).
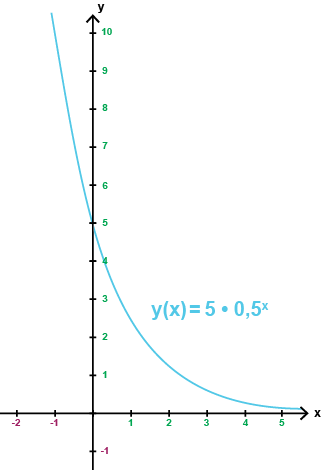
فيما يلي لدينا نظام إحداثيات به رسم بياني للدالة الأسية
$$y(x)=5\cdot 0,5^x$$
تحتوي هذه الدالة على أساس أصغر من 1 \((a = 0.5)\) وفي هذه الحالة تتناقص الدالة لجميع قيّم \(x\). كلما زادت قيمة \(x\) كلما اقتربت الدالة من محور \(x\) \((y = 0)\) ولكنها سوف لن تصل إلى محور \(x\).
باستخدام قاعدة القوة السالبة
$$a^{-x} = \frac{1}{a^{x}}$$
يمكن إعادة كتابة الدوال الأُسية التي تحتوي على أساس \(a\) أقل من 1 للحصول على دالة أُسية لها قوة سالبة (أو العكس).
إذا استخدمنا هذه العلاقة يمكن إعادة كتابة دالة المثال أعلاه على النحو التالي:
$$y(x)=5\cdot 0,5^x$$
$$y(x)=5\cdot \left ( \frac{1}{2} \right )^x$$
$$y(x)=5\cdot \, \frac{1}{2^x}$$
$$y(x)=5\cdot 2^{-x}$$
وبعبارة أخرى فإن \(y(x) = 5 \cdot 0,5^x\) هي نفس الدالة \(y(x) = 5 \cdot 2^{-x}\).
قيمة المعامل \(C\) في الدالة الأسية
تماما كما يتأثر شكل منحنى الدالة الأُسية بمقدار الأساس \(a\) سيتأثر بقيمة المعامل \(C\).
يمكن تفسير المعامل \(C\) على أنه عبارة عن قيمة الدالة عندما تساوي قيمة \(x\) الصفر \((x=0)\), أي قيمة الدالة عند نقطة تقاطع المنحنى مع المحور \(y\). فإذا عوضنا \(x=0\) في دالة أُسية أساسها \(a\) سنحصل على
$$y(0)=C\cdot a^0=C\cdot 1=C$$
الحل البياني للدوال الأُسية
فيما يلي مثال على الدالة الأُسية
$$y(x)=50000\cdot 1,02^x$$
هذه الدالة توضح مقدار المبلغ المالي \((y)\) في حساب مصرفي وذلك في حالة إيداع \(50\,000\) كرونة مع الحصول على فوائد سنوية بنسبة \(2\%\) (عامل التغيّر \(1.02\)), حيث أن \(x\) هو عدد السنوات بعد الإيداع.
إذا أردنا معرفة مقدار المبلغ المالي الذي لدينا في الحساب بعد 3 سنوات، فسنحتاج فقط لتعويض قيمة \(x\) بــ 3 ثم نحسب قيمة \(y\):
$$y(3)=50000\cdot 1,02^3 = 53060,40$$
بمعنى أن بعد 3 سنوات سيكون لدينا \(53\,060,40\) كرونة في الحساب.
إذا أردنا بدلا من ذلك معرفة كم عدد السنوات اللازمة لتوفير \(60\,000\) كرونة في الحساب, فيمكننا حلها بيانيا. هذه الطريقة التي سنستخدمها هنا هي نفس الطريقة التي استخدمناها في الكورس رياضيات 1 لحل المعادلات بيانيا.
يمكننا استخدام الدالة الأُسية لوصف هذه الحالة بحيث تكون قيمة \(y\) هي \(60\,000\) كرونة (أي سيكون هناك \(60\,000\) كرونة في الحساب).
$$50000 \cdot 1,02^{x} = 60000$$
لحل هذه المعادلة بيانيا سنقوم برسم الدوال التالية على نظام إحداثيات
$$y(x)=50000\cdot 1,02^x$$
$$y(x)=60000$$
ومن ثم نوجد إحداثي \(x\) لنقطة تقاطع الدالتين. قيمة إحداثي \(x\) هي الحل المطلوب لدالتنا الأُسية.
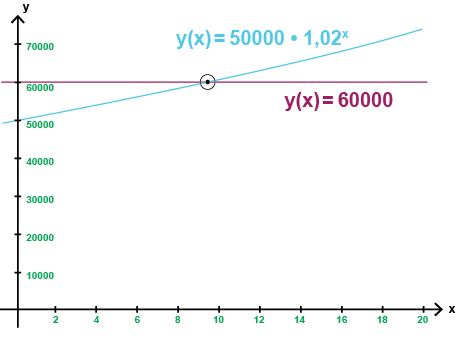
نلاحظ أن المنحنيين يتقاطعان عند \(x = 9.2\), ما يعني أنه سيكون لدينا \(60\,000\) كرونة في الحساب بعد \(9.2\) سنة.
ما قمنا به هنا هو حل معادلة أُسية بيانيا. بنفس الطريقة كما في حالة معادلات الدرجة الثانية يمكننا أيضا حل المعادلات الأُسية جبرياً، وهذا ما سندرسه في الأقسام القادمة.
فيديوهات الدرس (باللغة السويدية)
الدوال الأُسية ودوال القوى.
كيفية استخدام الدالة الأُسية كنموزج لنمو البكتريا.
