التوزيع الطبيعي
في القسم السابق تعلمنا كيفية حساب الانحراف المعياري, وهو مقياس للتشتُت حول القيمة المتوسطة (\(m\)). في هذا القسم سنتعرف على أحد الاستخدامات الشائعة للانحراف المعياري ألا وهو التوزيع الطبيعي.
عند قياس العديد من الظواهر الطبيعية والمجتمعية إتضح أن قيّم القراءات تميل إلى اتباع نمط (نموذج) معين وهو ما يُسمى بالتوزيع الطبيعي. قد يتعلق الأمر على سبيل المثال بأطوال الأشخاص البالغين سن الرشد، أوزان الأطفال حديثي الولادة، كمية مياه الأمطار النازلة خلال يوم من الأيام، الخ. تميل قيّم القراءات إلى أن تكون بالقرب من قيمة متوسطها (\(m\))، لكن كلما قل عدد القراءات المرصودة كلما ابتعدت من قيمة المتوسط. مثل هذه الظواهر يمكن وصفها باستخدام منحنى التوزيع الطبيعي، عندما يكون لدينا عدد كافئ من قيّم القراءات المرصودة يمكننا أن نتوقع شكل منحنى التوزيع الطبيعي كما في الشكل أدناه:
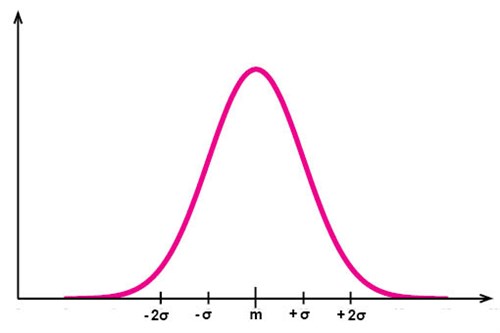
في منحنى التوزيع الطبيعي في الشكل أعلاه لدينا قيّم القراءات المرصودة على محور \(x\) وعلى محور \(y\) لدينا تكرار هذه القيّم (عدد مرات ظهورها في مجموعة القيّم).
أيضا تم تحديد مواقع القيّم على مسافات مختلفة من المتوسط (\(m\)) على محور \(x\). تعتمد هذه القيّم المحددة على قيمة الانحراف المعياري (\(\sigma\))، وهذا ما سنعود إليه قريبا.
عادة ما يكون منحنى التوزيع الطبيعي في شكل هضبة أو حدبة متماثلة. ومع ذلك تختلف أشكال منحنيات التوزيع الطبيعي إعتمادا على قيمتي المتوسط (\(m\)) والانحراف المعياري (\(\sigma\))، المتوسط هو الذي يحدد موقع المنحنى على محور \(x\) بينما الانحراف المعياري هو الذي يحدد شكل المنحنى (كلما قلت قيمة الانحراف المعياري كلما أعطى هضبة ضيقة مرتفعة وكلما زادت قيمته أعطى هضبة أوسع وأكثر انخفاضاً).
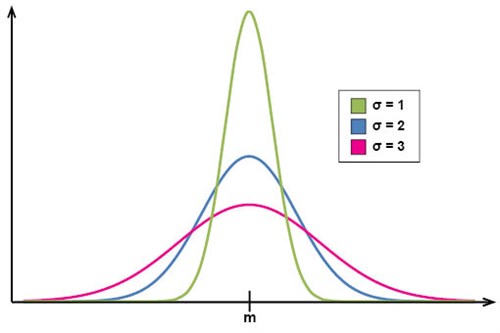
في الشكل التالي نلاحظ كيفية اختلاف شكل منحنى التوزيع الطبيعي وفقاً لقيّم الانحراف المعياري المقابلة. في حالة الانحراف المعياري الصغير نلاحظ أن قيّم القراءات بصورة عامة قريبة من قيمة المتوسط، بينما في حالة الانحراف المعياري الأكبر نلاحظ أن قيّم القراءات أكثر تشتُتاً من قيمة المتوسط:
بالنسبة لجميع القراءات الإحصائية الموزعة وفقا للتوزيع الطبيعي يكون لدينا \(50\%\) من قيّمها تقع تحت المتوسط، أي أقل منه و \(50\%\) من هذه القيم تقع فوق المتوسط، أي أكبر منه (لاحظ تماثُل منحنيات التوزيع الطبيعي حول المتوسط).
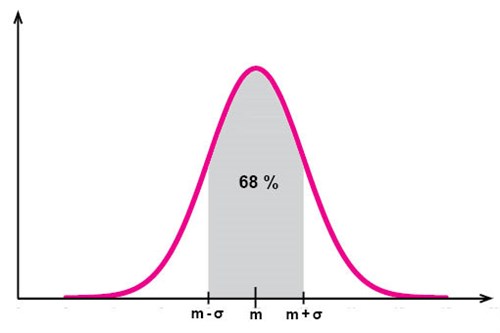
أيضا في حالة التوزيعات الطبيعية هنالك حوالي \(68\%\) من القيّم المرصودة متوزعة حول المتوسط على بعد مسافة تعادل قيمة الانحراف المعياري في كل اتجاه:
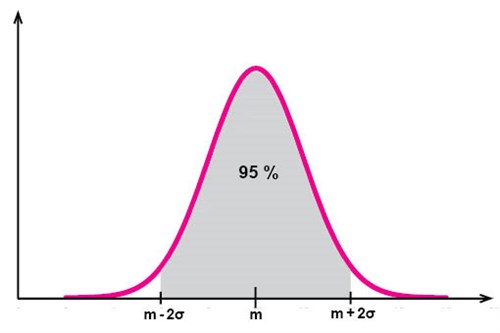
وحوالي \(95\%\) من القيّم المرصودة متوزعة حول المتوسط على بعد مسافة تعادل ضعف الانحراف المعياري في كل اتجاه:
دعونا ننظر إلى المثال التالي
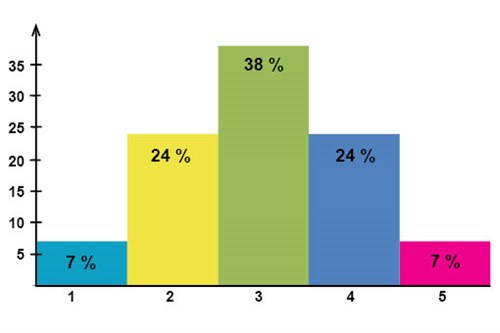
بين عامي 1966 و 1995 كانت المدارس الثانوية في السويد (من عام 1962 إلى عام 1994 في المدارس الابتدائية) تستخدم ما يُسمى بنظام التقييم بالدرجات النسبية. يعتمد نظام الدرجات النسبية بناءا على مفهوم توزيع مستوى المعرفة لدى الذين يدرسون نفس المادة توزيعا طبيعيا ولذلك ينطبق هذا أيضا على معدل الشهادة (النتيجة). كان تصنيف الشهادة (النتيجة) بمقياس درجات من 1 إلى 5, حيث أن \(7\%\) من الطلاب الذين يدرسون نفس المادة حصلوا على 1 وهو أقل معدل, \(24\%\) حصلوا على 2, \(38\%\) حصلوا على 3, \(24\%\) حصلوا على 4 و \(7\%\) حصلوا على 5 درجات وهو أعلى معدل.
للمقارنة بين جميع الطلاب في السويد الذين درسوا نفس المادة تم وضع امتحان مركزي (وهذا كان تمهيدا للامتحانات الوطنية الحالية). تم تصحيحها مركزيا وبناء على نتائج جميع طلاب السويد تم تحديد حدود الدرجات. تم انتقاد نظام تقييم الدرجات النسبية لأنه لا يقيس مستوى معرفة الطلاب الفعلية ولكنه يقيس مستوى الطلاب مقارنة بالطلاب الآخرين. أيضا تم انتقاد هذا النظام لأن العديد من المدارس استخدمت هذا النظام بطريقة خاطئة، حيث قام المعلمين بتطبيق التوزيع الطبيعي على كل فصل بصورة منفصلة. تم استبدال هذا النظام في عام 1996 بنظام درجات مبني على الهدف والمعرفة، حيث كانت هناك أهداف محددة لكل مستوى من مستويات الدرجات التي يجب تحقيقها للحصول على شهادة معينة.
فيديوهات الدرس (باللغة السويدية)
مفهوم التوزيع الطبيعي.
مثال على كيفية اجراء العمليات الحسابية للمواد الموزعة توزيع طبيعي.
