المعادلات الخطية الآنية - الحل البياني
في القسم السابق كررنا كيف يمكننا وصف العلاقات الخطية بين متغيرين باستخدام معادلات الخط المستقيم. في هذا القسم سنرى كيف يمكننا إيجاد نقطة تقاطع الخطوط المستقيمة وذلك من خلال حل معادلات هذه الخطوط آنياً.
المعادلات الآنية هي مجموعة من المعادلات المتزامنة، أي هي مجموعة من المعادلات التي تحتوي على نفس المتغيرات وقد تكون عبارة عن معادلتين أو أكثر. وهذا يعني أن حل المعادلات الآنية سيكون حلا لكل مجموعة المعادلات معا.
ولأن المعادلات الآنية تتكون من معادلتين خطيتين أو أكثر يُطلق عليها نظام المعادلات, وسُميت بالآنية لأنها عادة ما تكون متزامنة، أي تتحقق في آنٍ واحد.
وعادة ما تتم كتابة المعادلات الآنية بجانب قوس وفيما يلي لدينا مثال على كيفية كتابة معادلتين آنيتين:
$$\\\left\{\begin{matrix}y=k_1x+m_1\\ y=k_2x+m_2\end{matrix}\right.\\$$
يمكن حل المعادلات الخطية الآنية بعدة طرق مختلفة وسنبدأ بشرح حل المعادلات الخطية الآنية بيانيا.
الحل البياني
يمكن تفسير حل المعادلات الخطية الآنية بأنه هو عبارة عن نقطة تقاطع خطوط هذه المعادلات على نظام الإحداثيات.
يمكن حل نظام المعادلات الخطية بيانيا، إما برسمها يدويا أو باستخدام آلة حاسبة بيانية. هنالك العديد من الآلات الحاسبة البيانية التي تحتوي على برنامج رسم ويمكن استخدامها لحساب نقطة التقاطع (بالإنجليزية intercept).
دعونا ننظر إلى مثال على كيفية حل المعادلات الآنية بيانيا
فيما يلي لدينا معادلتين آنيتين:
$$\\\left\{\begin{matrix}y=2x+4\\ y=3x+2\end{matrix}\right.\\$$
الخطوة الأولى سنرسم الخطين على نظام إحداثيات. نُسمي قيمة \(y\) للخط الأول بــ \(L_1\) (الخط الأزرق) وقيمة \(y\) للخط الثاني بــ \(L_2\) (الخط الأحمر):
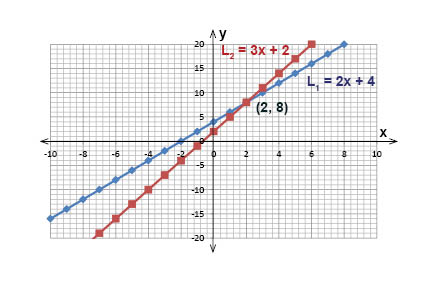
نلاحظ أن الخطان يتقاطعان في النقطة \((2, 8)\), وهذه النقطة هي حل لهاتين المعادلتين الآنيتين. أي أن الحل هو \(x = 2\) و \(y = 8\).
إذا عوضنا هذه القيّم في المعادلتين سنجد أن الطرف الأيسر يساوي الطرف الأيمن في كلا المعادلتين:
$$ \\\left\{\begin{matrix}8=2\cdot 2+4=4+4=8\\ 8=3\cdot 2+2=6+2=8\end{matrix}\right.\\$$
إذن الحل الذي توصلنا إليه هو حل صحيح.
عدد حلول المعادلات الخطية الآنية
في المثال أعلاه كان لدينا نقطة تقاطع واحدة وتحصلنا على حل واحد.
ولكن هناك حالات أخرى يمكن حدوثها عندما نتعامل مع نظام معادلات يتكون من معادلتان خطيتان آنيتان.
الحالة الأولى عندما يكون الخطان لهما نفس الميل \((k_1 = k_ 2 )\), أي عندما يكون الخطان متوازيان. في هذه الحالة سوف لن يتقاطع الخطان نهائيا وبالتالي ليس لدينا نقطة تقاطع - ولذلك نقول أن هذه المعادلات الآنية ليس له حل.
الحالة الثانية هي عندما ينطبق الخطان على بعضهما (أي أن الخطان يمكن وصفهما بنفس الميل \(k\) \((k_1 = k_2 )\) ونفس الجزء المقطوع \(m\) \((m_1 = m_ 2 )\) في معادلة الخط المستقيم) في هذه الحالة لدينا عدد لا نهائي من الحلول لهذه المعادلات, وذلك لأن كل نقطة تُمثل حلا لإحدى المعادلتين هي عبارة عن حل للمعادلة الأخرى أيضا.
احدى مشاكل الحل البياني لحل المعادلات الآنية هي صعوبة إيجاد الحل الدقيق في بعض الأحيان ويصبح الحل حل تقريبي. لحل المعادلة الآنية حل دقيق (بالضبط) قد يكون من الأفضل استخدام طريقة الحل الجبري. هناك نوعين من طرق الحل الجبري وهما: طريقة التعويض وطريقة الجمع كما سنناقشهما في الأقسام التالية.
فيديوهات الدرس (باللغة السويدية)
مقدمة عن المعادلات الآنية.
كيفية حل المعادلات الخطية الآنية بيانيا.
قيمة الميل \(k\) ومعناه في مفهوم المعادلات الآنية.
نواصل في شرح قيمة الميل \(k\) و الجزء المقطوع \(m\) ومعناهما في مفهوم المعادلات الآنية.
في هذا الفيديو أيضا نواصل في شرح أهمية قيمتي الميل \(k\) والجزء المقطوع \(m\) في مفهوم المعادلات الآنية.
كيف يمكننا حل المعادلات الآنية و المتباينات بيانيا.
كيفية حل المعادلات الآنية بيانيا.
