مُنصّف الزاوية

هذا القسم يدخل في مقرر كل من رياضيات 2b ورياضيات 2c.

مُنَصّف الزاوية هو عبارة عن خط مستقيم يقوم بتقسيم الزاوية الى نصفين. في الشكل أدناه الخط AD هو عبارة عن منصّف زاوية وذلك لأن الزاوية BAD تساوي الزاوية CAD (أي أن كل منهما يُمثل نصف الزاوية BAC).

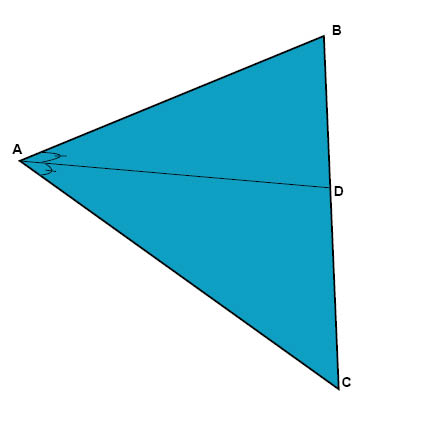
تنص نظرية زاوية المُنصّف على أن منصّف الزاوية يُقسّم الضلع المقابل لهذه الزاوية وفقا للعلاقة التالية:

$$\frac{BD}{CD}=\frac{AB}{AC}$$

الإثبات

لإثبات صحة نظرية مُنصّف الزاوية سنبدأ بتمديد المُنصّف إلى النقطة P, بحيث تكون المسافة AB مساوية للمسافة BP كما في الشكل أدناه ويكون لدينا مثلث متساوي الساقين وهو \(\triangle ABP\).

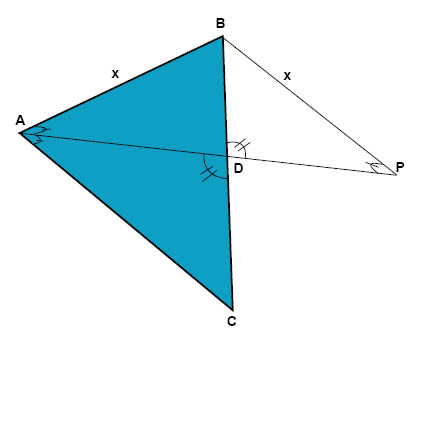
من الشكل نلاحظ أن الزاوية BAD تساوي الزاوية BPD لأنهما زاويتي قاعدة المثلث المتساوي الساقين ABP.

وبما أن الخط AP هو مُنصّف الزاوية BAC وفقا للتعريف سيكون لدينا أيضا أن الزاويتين BAD و CAD متساويتين.

الزاويتان BDP و ADC أيضا متساويتان لأنهما متقابلتان بالرأس.

ولأن المثلث ACD له زاويتان ولكل منهما زاوية مساوية في المثلث BDP فهذا يعني أنهما مثلثان متشابهان وبما أن المثلثان متشابهان يمكن كتابة العلاقة بين الأضلاع المتقابلة لهاذين المثلثين كما يلي:

$$\frac{DC}{BD}=\frac{AC}{BP}$$

وبما أن \(BP = AB\), بالتالي يمكننا الحصول على

$$\begin{align} \frac{DC}{BD} = & \frac{AC}{AB}\\ & \\ \iff &  \\ & \\ \frac{BD}{DC}= & \frac{AB}{AC} \end{align}$$

وهو المطلوب إثباته.

فيديو الدرس (باللغة السويدية)

شرح إثبات صحة نظرية مُنصّف الزاوية.