المستقيمات القاطعة
هذا القسم يدخل في مقرر كل من رياضيات 2b ورياضيات 2c.
يُسمى الخط المستقيم الذي يقطع ضلعين من أضلاع المثلث بالمستقيم القاطع. إذا كان هذا المستقيم القاطع موازيا للضلع الثالث في المثلث، في هذه الحالة يُسمى بالمستقيم القاطع الموازي.
باستخدام مفهوم القاطع المستقيم الموازي يمكننا صياغة: نظرية مثلث القمة ونظرية المستقيم القاطع الهندسيتين وهذا ما سنشرحه في هذا القسم.
الخط DE في الشكل أدناه هو عبارة عن مستقيم قاطع موازي للمستقيم CB في المثلث ABC. المثلث ADE يُسمى بمثلث القِمة.
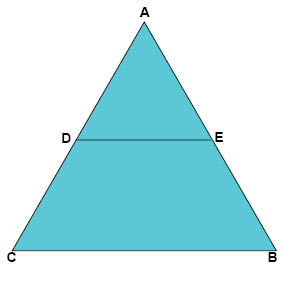
نظرية مثلث القِمة
تنص نظرية مثلث القمة على أن مثلث القِمة (المثلث ADE في الشكل أعلاه) المُتكون بواسطة المستقيم القاطع الموازي هو مثلث متشابه مع المثلث الكبير (المثلث ABC).
$$\bigtriangleup ADE\sim \bigtriangleup ABC$$

الإثبات
لإثبات صحة نظرية مثلث القمة يجب إثبات\بُرهان أن المثلثين ADE و ABC متشابهين. تعريف التشابه ينص على أن إذا كان هناك زاويتين في المثلث ADE ولكل منهما زاوية مساوية في المثلث ABC فإن المثلثان متشابهان.
فإذا أثبتنا أن هناك زاويتين في المثلث ADE ولكل منهما زاوية مساوية في المثلث ABC فهذا يعني أننا أثبتنا أن المثلثين متشابهين وهو إثبات لصحة نظرية مثلث القِمة.
الزاوية A هي زاوية مشتركة في المثلثين وهذا يعني أن
$$\measuredangle DAE=\measuredangle CAB$$
بالإضافة الى ذلك يمكننا ايجاد العلاقة بين الزاويتين \(\measuredangle AED\) و \(\measuredangle ABC\) ونتحقق من أنهما متساويتين أم لا. سنبدأ بتوضيح مفهوم الزوايا المتناظرة.
الزوايا المتناظرة: عندما يقطع أي خط مستقيم خطان فإن الزاويا الواقعة بنفس جانب هذا المستقيم القاطع وبنفس الجانب بالنسبة للخطان المقطوعان تُسمى بالزوايا المتناظرة. أي الزوايا التي تأخذ مواضع متشابهة في نقاط التقاطع. وعندما يكون الخطان المقطوعان متوازيان فإن الزاويتان المتناظرتان متساويتان.
الآن نعود للإثبات. في المثلث ABC نعلم أن الخط DE موازي للضلع CB, وهذا يعني أن الزاويتين \(\measuredangle AED\) و \(\measuredangle ABC\) زاويتان متساويتان بالتناظر:
$$\measuredangle AED=\measuredangle ABC$$
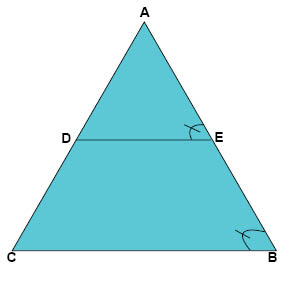
وبما أن لدينا مثلث به زاويتين ولكل منهما زاوية مقابلة ومساوية في المثلث الآخر فهذا يعني أن جميع الزوايا المتقابلة في المثلثين متساوية مما يعني أن المثلثان متشابهان.
$$\bigtriangleup ADE\sim \bigtriangleup ABC$$
وهو المطلوب إثباته.
نظرية المستقيم القاطع
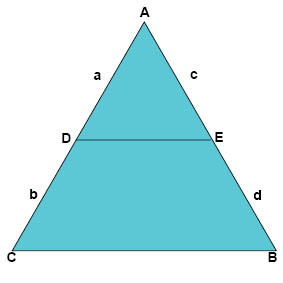
نظرية المستقيم القاطع تنص على أن المستقيم القاطع الموازي الذي يقطع ضلعين من أضلاع المثلث سيقطع الضلعين بنفس النسبة، ما يعني
$$\frac{a}{b}=\frac{c}{d}\;\;\textbf{أو}\;\;\frac{b}{a}=\frac{d}{c}$$
وذلك باستخدام رموز أضلاع المثلثين الموضحة في الشكل أدناه.
الإثبات
من برهان نظرية مثلث القِمة أعلاه نعلم أن الزاويتين AED و ABC متساويتين وأيضا الزاويتين ADE و ACB متساويتين وذلك لأن المثلث الكبير ومثلث القمة (الصغير) متشابهين.
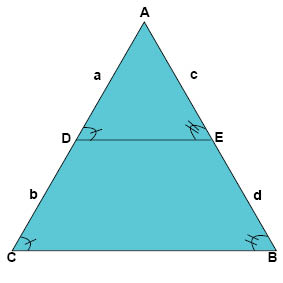
وبما أن المثلثين متشابهين فإن النسب بين الأضلاع المتقابلة متساوية، أي أن
$$\frac{a+b}{a}=\frac{c+d}{c}$$
يمكننا تبسيط هذا التعبير بضرب الطرفين فـي \(ac\):
$$\frac{ac\cdot \left (a+b \right )}{a}=\frac{ac\cdot \left (c+d \right )}{c}$$
$$c\cdot(a+b)=a\cdot(c+d)$$
الآن يمكننا المواصلة في تبسيط التعبير بضرب كل من c و a فـي ما بداخل القوسين.
$$c\cdot(a+b)=a\cdot(c+d)$$
$${\color{Red} \not}{ac}+ bc={\color{Red} \not}{ac}+ad$$
$$bc=ad$$
$$\frac{a}{b}=\frac{c}{d}$$
هذا هو الجزء الأول من النظرية. يمكننا الحصول على الجزء الثاني من النظرية بإعادة كتابة الجزء الأول كما يلي:
$$\frac{a}{b}=\frac{c}{d}$$
$$\frac{a\cdot {\color{Blue} {b\cdot d}}}{b}=\frac{{\color{Blue} b}\cdot c\cdot {\color{Blue} d}}{d} \Rightarrow$$
$$a\cdot d=b\cdot c$$
$$\frac{a\cdot d}{{\color{Blue} {a\cdot c}}}=\frac{b\cdot c}{{\color{Blue} {a\cdot c}}} \Rightarrow$$
$$\frac{d}{c}=\frac{b}{a}$$
وهو المطلوب إثباته.
فيديوهات الدرس (باللغة السويدية)
مفاهيم الزوايا المتجاورة, المتقابلة بالرأس, المتبادلة و المتناظرة.
نظرية المستقيم القاطع.
مثال على نظرية مثلث القِمة.
أستخدام الآلة الحاسبة
هنا تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس المثال على الآلة الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.
