علاقة الارتباط وتحليل الانحدار
في هذا القسم سندرس اثنين من المفاهيم المرتبطة ببعضها وهما مفهومي علاقة الارتباط وتحليل الانحدار. باستخدام هاذين المفهومين يمكننا إيجاد علاقة لسلسلة من القراءات (القيّم) الاحصائية، هذه العلاقة يمكن استخدامها في دراسة الظواهر بصورة أفضل في العديد من السياقات المختلفة.
علاقة الارتباط (Korrelation)
تم إجراء دراسة احصائية بحساب عدد الأشخاص الموجودين على رصيف إحدى محطات القطار وذلك ما بين الساعة التاسعة الى العاشرة صباحا في يوم الإثنين الأول من كل شهر لمدة سنة كاملة. وكانت النتائج عند نهاية السنة كما في الجدول أدناه.
| الشهر | عدد الأشخاص | الشهر | عدد الأشخاص |
| يناير (jan) | 20 | يوليو (jul) | 79 |
| فبراير (feb) | 100 | أغسطس (aug) | 122 |
| مارس (mar) | 105 | سبتمبر (sep) | 180 |
| أبريل (apr) | 97 | أكتوبر (okt) | 116 |
| مايو (maj) | 205 | نوفمبر (nov) | 99 |
| يونيو (jun) | 158 | ديسمبر (dec) | 86 |
يمكن استخدام مخطط تشتُت بياني بحيث يكون متغير التوضيح (المتغير المُستقل) على محور \(x\) والمتغير الناتج (التابع) على محور \(y\). في هذا المثال، الشهر هو متغير التوضيح وعدد الأشخاص على الرصيف هو المتغير الناتج. لكل قيمة من قيّم متغير التوضيح تم تحديد القيمة المقابلة للمتغير الناتج على الرسم (في هذه الحالة لدينا على سبيل المثال الشهر "مارس" كقيمة من قيّم متغير التوضيح وقيمة المتغير الناتج المقابلة هي 105 شخص). من سلسلة هذه القيّم المرصودة يمكننا البحث عن علاقة ما تربط بين الشهر وعدد الأشخاص الذين كانوا على رصيف محطة القطار. وذلك برسم مخطط تشتُت بياني للقيّم المرصودة.
على رسم المخطط البياني لهذا المثال تم تحديد كل نقطة احداثية (قيمتي متغير التوضيح والمتغير الناتج) بعلامة مربع صغير كما يلي:
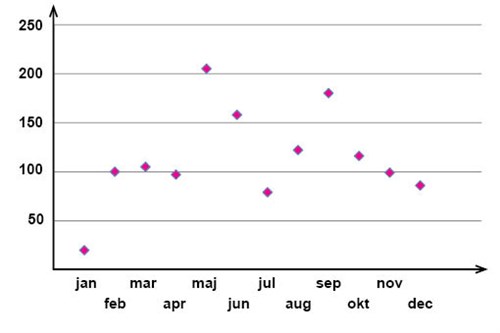
من خلال دراسة مخطط التشتُت يمكن استنتاج ما إذا كان هنالك علاقة تربط بين متغير التوضيح والمتغير الناتج أم لا.
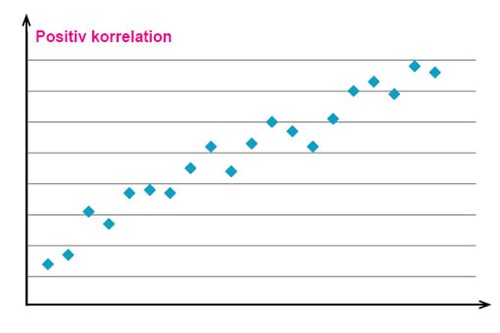
إذا كانت قيّم القراءات المرصودة التي تم تحديدها على مخطط التشتُت متجمعة حول خط خيالي ميله موجب عندها نقول أن هنالك علاقة ارتباط ايجابية (Positiv korrelation) بين متغير التوضيح (المُستقل) والمتغير الناتج (التابع). وهذه الحالة تنطبق على سلسلة القراءات الموضحة على الرسم البياني أدناه.
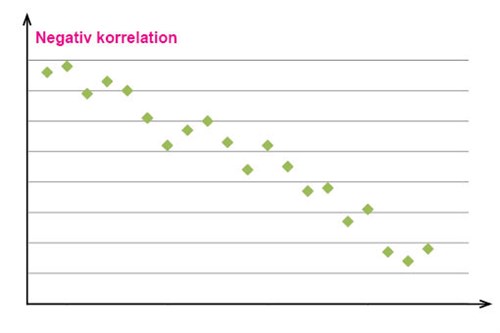
أما إذا كانت قيّم القراءات المرصودة متجمعة حول خط خيالي ميله سالب عندها سنقول أن هنالك علاقة ارتباط سلبية (Negativ korrelation) بين متغير التوضيح والمتغير الناتج ويمكن ملاحظة ذلك في الرسم البياني أدناه.
في حالة المثال الأول في بداية هذا القسم لا يبدو أن هناك أي علاقة ارتباط ايجابية أو سلبية بين المتغيرين وفي هذه الحالة نقول أن علاقة الارتباط مفقودة ومن قيّم القراءات المرصودة في هذا المثال يمكننا خلاصة أن ليست هناك أي علاقة بين الشهر وعدد الأشخاص الواقفين على الرصيف.
عندما نريد فقط دراسة علاقات الارتباط بين متغيرات معينه من المهم أن نتذكر أنه ليست بالضرورة وجود علاقة سببية وهذا يعني أن إذا كان هنالك علاقة ارتباط بين متغيرات معينه فقد يكون هنالك متغير آخر خفي (غير مذكور في عملية التحليل) يوضح عملية تزامن تغيّرها.
إذا أجرينا على سبيل المثال دراسة مقارنة بين العمر وحدوث مرض معين قد تكون هناك علاقة ارتباط إيجابية قوية بين عمر الشخص ومدى انتشار المرض. ومع ذلك لا يمكننا استنتاج أن التقدم في العمر هو سبب المرض بكل بساطة، فقد توجد عوامل أخرى لها دور في ذلك كالعادات المعيشية، وجود أمراض أخرى، عادات الأكل اليومية السابقة وما شابه ذلك. لذلك يجب أن نكون حَذِرين عند استنتاج العلاقات السببية التي تربط بين المتغيرات المُراد دراستها.
تحليل الانحدار (Regressionsanalys)
من رسم مخطط التشتٌت الذي يحتوي على علاقة خطية (علاقة ارتباط ايجابية أو سلبية) يمكننا وصف العلاقة باستخدام النموذج الخطي، بعبارة أخرى يمكن وصف العلاقة باستخدام معادلة الخط المستقيم كما في الصيغة التالية
$$y = kx + m$$
عملية إيجاد النموذج الخطي الذي يصف العلاقة بين المتغيرات تُسمى بالانحدار الخطي أو تحليل الانحدار. بمعنى أن الخط الذي نبحث عنه يختلف أو يتباعد عن النقاط المحددة على الرسم اقل اختلاف (تباعُد) ممكن. فاذا كان لدينا رسم تشتُت يمكننا رسم هذا الخط التقريبي باليد ومن ثم نوجد قيمتي الميل \(k\) والجزء المقطوع \(m\) لهذا الخط باستخدام النقاط التي يمر بها الخط كما رأينا سابقا. معادلة الخط المستقيم التي نبحث عنها غالبا ما تُسمى بالمعادلة المناسبة، حيث أن هذا الخط المستقيم ينحرف عن النقاط المحددة (قيّم القراءات) على الرسم أقل انحراف ممكن.
للحصول على خط الانحدار المناسب بصورة دقيقة قدر الإمكان يمكن على سبيل المثال استخدام الآلات الحاسبة البيانية التي تحتوي على دوال رسم.
عند إيجاد المعادلة الخطية المناسبة لوصف بياناتنا الاحصائية باستخدام تحليل الانحدار يمكن بعد ذلك استخدام هذا النموذج الخطي للتنبؤ بما سنحصل عليه من قيّم القراءات الأخرى.
متوسط طول الأطفال السويديين
في مخطط التشتُت أدناه قمنا بتحديد متوسط الطول (المتغير الناتج) للأطفال السويديين على محور \(y\) والذيّن تتراوح أعمارهم بين 1-16 سنة (متغير التوضيح) على محور \(x\).
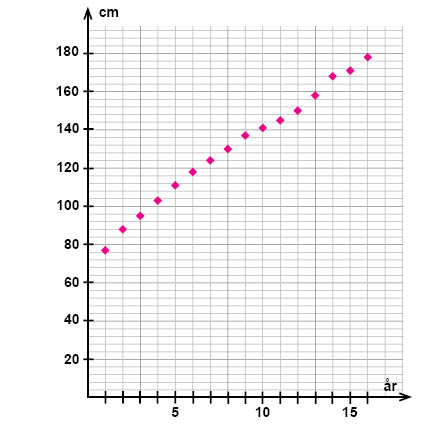
كما نلاحظ يبدو أن هنالك علاقة ارتباط خطية ايجابية بين العمر ومتوسط الطول ولذلك يمكننا أن نحاول إيجاد نموذج خطي لهذه العلاقة باستخدام تحليل الانحدار الخطي.
نبدأ برسم خط مستقيم بحيث يكون متقارب من جميع النقاط بقدر الإمكان، أي أن الانحراف بين الخط والنقاط صغير بقدر الإمكان كما في الشكل التالي.
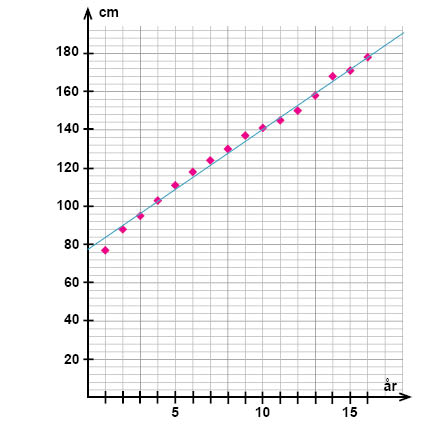
الآن لدينا خط مستقيم موضح على مخطط التشتُت ويمكننا قراءة احداثيات أي نقطتين (اختيار عشوائي) على طول هذا الخط كما في حالة أي خط مستقيم آخر. هاذان النقطتان ليس من الضروري أن تكونا من النقاط المحددة على الرسم البياني؛ يمكن قراءة أي نقطتين يبعُدان عن بعضهما البعض بمسافة مناسبة على طول الخط لكي تصبح أخطاء القراءة أقل أهمية.

في مخطط التشتُت أعلاه تم تحديد النقطتين \((4; 102,5)\) و \((15; 172)\).
بعد الحصول على إحداثيات نقطتين على امتداد الخط، يمكننا استخدام هذه الإحداثيات لحساب ميل هذا الخط:
$$k=\frac{172-102,5}{15-4}=\frac{69,5}{11}\approx6,3$$
في الخطوة التالية يمكننا ايجاد معادلة هذا الخط المستقيم وذلك باستخدام صيغة الميل \(k\) أو صيغة النقطة المعلومة.
في هذا المثال سنستخدم صيغة الميل \(k\)، بتعويض احدى قيّم احداثيات النقطتين أعلاه يمكننا حساب قيمة الثابت \(m\):
$$y=kx+m$$
$$172=\frac{69,5}{11}\cdot 15+m$$
$$m=172-\frac{69,5\cdot 15}{11}\approx77$$
بعد إيجاد قيمتي معامل الاتجاه (الميل) \(k\) والحد الثابت (الجزء المقطوع) \(m\) يمكننا الحصول على معادلة الخط المستقيم المطلوبة:
$$y=6,3x+77$$
بالتالي هذه هي العلاقة الخطية بين العمر \(x\) ومتوسط الطول \(y\) التي استنتجناها من البيانات الإحصائية المُعطية.
كما ذكرنا سابقا يمكننا استخدام الانحدار الخطي لتوقُع القيّم المستقبلية، أي يمكننا بالتقريب معرفة أطوال الأطفال بصورة عامة وفقا لأعمارهم. يمكننا على سبيل المثال معرفة طول الطفل (بالتقريب) الذي يبلغ من العمر 13 عاما باستخدام هذه العلاقة الخطية:
$$y(13)=6,3\cdot 13+77=158,9\,cm$$
إذا تم التحليل بصورة صحيحة فإن الانحدار الخطي سيعمل بصورة جيّدة في النطاق أو الفترة التي تمت دراستها أو حتى خارج هذا النطاق بقليل في أغلب الأحيان ولكن بالطبع كلما ابتعدنا من النطاق الذي تم استنتاج الانحدار الخطي منه بكثير كلما كانت نتائجه أسوأ. مثلا إذا استخدمنا هذا النموذج الخطي أعلاه لمعرفة طول شخص عمره 50 عاما عندها سنحصل على
$$y(50)=6,3\cdot 50+77=392\,cm$$
أي أن الشخص الذي عمره 50 عاما سيكون طوله حوالي 3.92 متر وفقا لهذا النموذج، وهذا يؤكد أن هذا النموذج غير مناسب للكبار (لأن الناس عادة ما يتوقف نمو طولهم في عمر الــ 18 الى 20 سنة تقريبا).
ومن المرجح أيضا أن يكون هذا النموذج الخطي غير مناسب لتقدير أطوال الأطفال الصغار جدا كحديثي الولادة، أي الذين عمرهم 0 سنة (كما يمكننا أيضا أن نتخيل الوضع بالنسبه للذين أعمارهم 1 سنة بالنظر لمخطط التشتُت). وفقا لهذا النموذج فان حديث الولادة (عمر 0 سنة) سيكون طوله 77 سم، ولكن في الواقع متوسط طول الأطفال حديثي الولادة هو 50 سم.
فيديو الدرس (باللغه السويدية)
تحليل الانحدار وعلاقة الارتباط.
استخدام الآلة الحاسبه
هنا تم استخدام الآله الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآله الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريباً.
