اللوغاريتمات العشرية
هذا القسم يدخل في مقرر كل من رياضيات 2b ورياضيات 2c.
في القسم السابق ألقينا نظرة على كيفية عمل الدوال الأُسية وكيفية حلها بيانيا. وفي هذا القسم سنتعلم كيف يمكننا حل المعادلات الأُسية جبريا من خلال استخدام اللوغاريثمات.
سنبدأ نقاش هذا الموضوع برسم الدالة الأُسية التالية بيانياً
$$y = 10^{x}$$
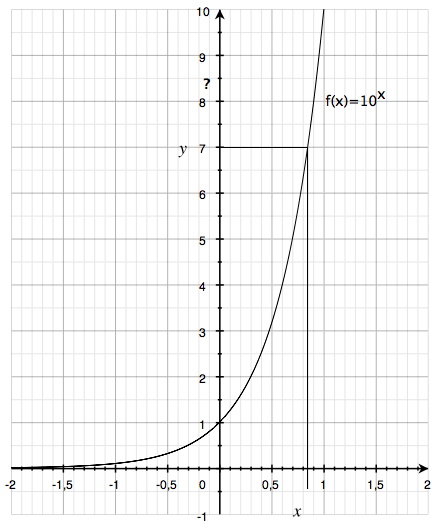
في نظام الإحداثيات أعلاه اخترنا نقطة من نقاط المنحنى، حيث أن \(y= f (x) = 7\) وبقراءة محور \(x\) سنجد أنه عندما تكون \(y = 7\) فإن \(x \approx 0.85\) وبالتالي سيكون لدينا
$$10^{0,85} \approx 7$$
يمكننا أخذ أي قيمة موجبة على محور \(y\) وقراءة قيمة \(x\) المقابلة لها على المنحنى. يمكن أعادة كتابة أي عدد بحيث يصبح قوة ذات الأساس 10, أي قوى العدد عشرة. على سبيل المثال
| $$10^{0}=1$$ | $$10^{0,78}=6$$ |
| $$10^{0,3}=2$$ | $$10^{0,85}=7$$ |
| $$10^{0,48}=3$$ | $$10^{0,9}=8$$ |
| $$10^{0,6}=4$$ | $$10^{0,95}=9$$ |
| $$10^{0,7}=5$$ | $$10^{1}=10$$ |
العدد الذي يجب رفعه كقوة (أُس) للعدد 10 لكي نحصل على العدد الموجب \(y\) يُسمى باللوغاريثم العشري للعدد \(y\). وهذا يعني أن اللوغاريثم العشري للعدد 9 هو تقريبا \(0,95\) والذي يمكن قراءته من الجدول أعلاه.
إذا كان لدينا معادلة أُسية، على سبيل المثال
$$11 = 10^{x}$$
ونريد حلها، يمكننا حلها بيانيا، أي برسم المنحنى \(10^x\) بيانيا، ومن ثم نقرأ قيمة \(x\) عندما تكون \(y = 11\) (تماما كما فعلنا في المثال أعلاه وفي قسم الدوال الأُسية السابق).
البديل الآخر لحل هذه المعادلة هو استخدام الآلة الحاسبة. العديد من الآلات الحاسبة تحتوي على برنامج جاهز لحل هذا النوع من المسائل وتعطي نفس النتائج التي سنحصل عليها من رسم الدالة وقراءة الحل بيانيا. يُسمى هذا البرنامج على لوحة الآلة الحسابة بــ "log" أو "lg" (فيما يلي سنرمز للوغاريثم بــ "lg" ولكن أيضا يمكن استخدام "log")
حل المعادلة
$$11 = 10^{x}$$
هو كما يلي
$$x = lg \:11 \approx 1,04$$
تعريف اللوغاريثم العشري
تعريف اللوغاريتم العشري هو كما يلي:
$$y = 10^{x} \Leftrightarrow x = lg \:y\: \: \: \: \:(y > 0)$$
يمكن إعادة كتابة جميع الأعداد الموجبة في صورة أُسية أساسها العدد 10, وذلك لأن
$$x = 10^{lg\:x}$$
وبصورة عامة يمكننا كتابة أي عدد موجب \(a\) كما يلي:
$$a = 10^{lg\:a}$$
على سبيل المثال يمكننا كتابة
$$5 = 10^{lg\:5}$$
إمكانية استخدام تعريف اللوغاريثم العشري وإعادة كتابة الأعداد الموجبة في صورة أُسية أساسها العدد 10 مفيدة جدا في حل المعادلات الأُسية جبرياً.
حل المعادلات الأُسية باستخدام اللوغاريثم العشري
لنرجع الآن إلى مثال المعادلة الأُسية التي قمنا بحلها بيانياً في قسم الدوال الأُسية السابق ونحاول حلها جبرياً باستخدام اللوغاريثم العشري.
في ذلك المثال أودعنا \(50\,000\) كرونة في حساب مصرفي بمقابل فوائد مالية بنسبة \(2\%\), وكان السؤال إيجاد الفترة الزمنية اللازمة لادخار \(60\,000\) كرونة في الحساب.
ووفقا لهذه المُعطيات تم استخدام المعادلة الأُسية التالية:
$$50000\: \cdot 1,02^{x }= 60000$$
حل هذه المعادلة هو ايجاد قيمة \(x\) وهي التي تُمثل عدد السنوات اللازمة لترك الأموال في الحساب بدون أي سحب لكي تصبح \(60\,000\) كرونة.
تماما كما في حالة حَل المعادلات الأخرى سنحاول وضع المتغير \(x\) وحده في أحد طرفي المعادلة. لذا سنبدأ بترك الصورة الأُسية لوحدها فقط في الطرف الأيسر وذلك بقسمة طرفي المعادلة علـى \(50\,000\):
$$\frac{50000\:\cdot 1,02^{x}}{50000} = \frac{60000}{50000} $$
$$1,02^{x} = 1,2$$
الآن يمكننا إعادة كتابة طرفي هذه المعادلة الأُسية باستخدام تعريف اللوغاريثم العشري، أي بكتابة العددين 1.02 و 1.2 في صورة أُسية أساسها العدد 10:
$$1,02 = 10^{lg\:1,02} $$
$$1,2 = 10^{lg\:1,2}$$
الآن نعوض هذه القيّم الأُسية للعددين 1.02 و 1.2 في المعادلة الأُسية:
$$(10^{lg\:1,02})^{x} = 10^{lg\:1,2}$$
نلاحظ أن الطرف الأيسر يحتوي على أُسيّن (أُس الأُس)، باستخدام قوانين القوى (الأُسُس) يمكننا إعادة كتابة الطرف الأيسر بضرب القوتين في بعضهما \((x \cdot lg 1,02)\) بحيث تصبح المعادلة
$$10^{x\cdot lg1,02} = 10^{lg\,1,2}$$
وبما أن طرفي هذه المعادلة لهما نفس الأساس فيجب أن تكون القوتين متساويتين.
أي أن:
$$x \cdot lg\:1,02 = lg \ 1,2$$
من هنا يمكننا إيجاد قيمة \(x\) باستخدام الآلة الحاسبة:
$$\frac{x\cdot lg\,1,02}{{\color{Blue} {lg\,1,02}}}=\frac{lg\,1,2}{{\color{Blue} {lg\,1,02}}}$$
$$x=\frac{lg\,1,2}{lg\,1,02}\approx9,2$$
إذن سيصبح لدينا في الحساب المصرفي \(60\,000\) بعد 9.2 سنة تقريباً.
نلاحظ أن الحل الجبري لهذه المعادلة الأُسية باستخدام اللوغاريثم العشري هو نفس الحل البياني. وبهذه الطريقة الجبرية تمكنا من إيجاد الحل الدقيق بدلاً من التقريب وذلك بكتابة الحل في صورة نسبة بين لوغاريثمين عشريين.
فيديوهات الدرس (باللغة السويدية)
مفهوم اللوغاريثم العشري.
مثال على اللوغاريثم العشري.
