الدوال الخطية
في الكورس رياضيات 1 قمنا باستخدام معادلة الخط المستقيم لوصف أنواع معينة من العلاقات. في هذا القسم سنكرر أساسيات الدوال الخطية ونواصل في بناء هذا المفهوم لكي نستخدمه لاحقا في قسم حل المعادلات الخطية الآنية القادم.
كما ذكرنا سابقا الدالة هي عبارة عن علاقة بين متغيرين أو أكثر، بحيث أن لكل قيمة من قيّم المتغير المُستقل (أو عدة متغيرات مُستقلة) يمكننا دائما إيجاد قيمة المتغير التابع المقابلة.
الدالة الخطية هي الدالة التي يكون شكلها على نظام الإحداثيات عبارة عن خط مستقيم ويمكن وصفها باستخدام صيغة معادلة الخط المُستقيم:
$$y=kx+m$$
حيث أن \(x\) و \(y\) متغيران و \(k\) و \(m\) ثوابت؛ \(k\) هو ميل الخط و \(m\) هي الجزء الذي يقطعه الخط من محور \(y\) (أي النقطة التي يقطع فيها هذا الخط محور \(y\) وذلك عند \(x = 0\)).
يمكن تفسير ميل الخط المستقيم على نظام الإحداثيات بأنه إذا تحركنا ابتداءاً من الخط سنجد أن كل خطوة نتحركها في اتجاه \(x\) الموجب ستحتاج الى \(k\) خطوة في اتجاه \(y\) الموجب للعودة مرة أخرى للخط. فإذا كانت قيمة \(k\) على سبيل المثال تساوي 2 فهذا يعني أن زيادة قيمة \(x\) بمقدار 1 تعني أن زيادة قيمة \(y\) بمقدار 2. أما إذا كانت قيمة \(k\) هي \(-3\) فهذا يعني أن زيادة قيمة \(x\) بمقدار 1 يؤدي إلى انخفاض قيمة \(y\) بمقدار 3 (لأن \(k\) تساوي \(-3\)).
دعونا نأخذ مثال
نفترض أن لدينا الدالة
$$y=2x+3$$
إذا رسمنا جزء من مخطط هذه الدالة على نظام إحداثيات سنجده كما يلي:
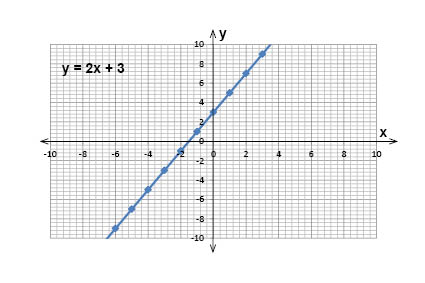
سنلاحظ أن خط هذه الدالة على نظام الإحداثيات سيتقاطع مع محور \(y\) عندما تكون \(y = 3\) وهي قيمة \(m\) تماما كما في المعادلة.
إذا انتقلنا خطوة في اتجاه \(x\) سننتقل خطوتين في اتجاه \(y\) للوصول إلى نقطة على الخط، مما يعطينا أن قيمة الميل هي \(k = 2\):
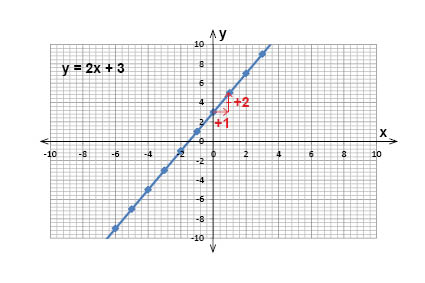
ميل الخط
يمكن تسمية قيمة الميل \(k\) بمعامل الاتجاه ويمكن حساب هذه القيمة بالصيغة التالية
$$k=\frac{\textsf{y التغير في}}{\textsf{x التغير في}}=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
لحساب قيمة \(k\) (الميل) لخط ما باستخدام هذه الصيغة سنحتاج لمعرفة إحداثيات نقطتين مختلفتين على هذا الخط \(( x_1, y_1)\) و \((x_2, y_2)\).
الخطان اللذان لهما نفس الميل (قيمة \(k\)) يكونان متوازيان:
$$k_{1}=k_{2}$$
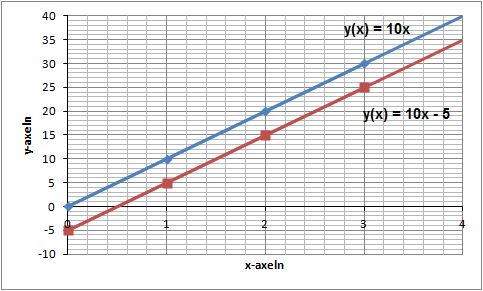
الخطان في الشكل أعلاه متطابقان والبُعد بينهما عبارة عن خمس خطوات، أي أن الخط السفلي يبعد عن الخط العلوي بخمس خطوات في الاتجاه السالب لــ \(y\) وهذا يُمثل قيمة \(m\) وهي المسافة التي تفصل بينهما (في الحالة الأولى \(m = 0\) وفي الحالة الثانية \(m = 5\)) وبما أن الخطين لهما نفس قيمة \(k\) فهذا يعني أن الخطان متوازيان.
أيضا لكل خطان متعامدان على بعضهما، أي أن الزاوية بينهما قائمة نجد أن
$$k_{1}\cdot k_{2}=-1$$
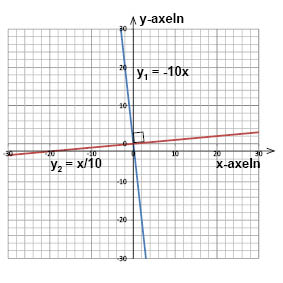
في الشكل أعلاه لدينا خطان متعامدان وذلك لأن حاصل ضرب قيمتي \(k\) لهذان الخطان يساوي \(-1\) وفقا للصيغة التالية
$$k_1\cdot k_2=-10\cdot \frac{1}{10}=-\frac{10}{10}=-1 $$
إيجاد معادلة الخط المستقيم باستخدام نقطتين معلومتين
فيما يلي سنرى كيف يمكننا إيجاد معادلة الخط المستقيم بمعلومية نقطتين من النقاط التي يمر بها هذا الخط.
لنفترض أننا نريد إيجاد معادلة الخط المستقيم الذي يمر بالنقطتين \((1, 5)\) و \((3, 4)\) والتي تأخذ الصيغة:
$$y=kx+m$$
لإيجاد هذه المعادلة سنحتاج لحساب قيمة كل من \(k\) و \(m\). وبذلك يكون لدينا علاقة تصف جميع النقاط التي تقع على هذا الخط.
نبدأ بإيجاد قيمة \(k\) وذلك بتعويض قيّم إحداثيات النقطتين في صيغة الميل التي تمت صياغتها أعلاه في هذا القسم:
$$k=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{4-5}{3-1}=-\frac{1}{2}$$
الآن بعد الحصول على قيمة \(k\) لهذا الخط وصلنا إلى منتصف الطريق وسيكون شكل المعادلة كما يلي:
$$y=-\frac{1}{2}x+m$$
بعد الوصول إلى هذه الخطوة سيكون لدينا طريقتين مختلفتين لإيجاد قيمة \(m\). تُسمى الطريقة الأولى بصيغة الميل-\(k\) وتُسمى الطريقة الأخرى بصيغة النقطة المعلومة. فيما يلي سنشرح الطريقتين بحيث يمكنك اختيار الطريقة التي تُناسبك.
صيغة الميل-\(k\)
لإيجاد قيمة \(m\) لأي دالة خطية باستخدام صيغة الميل-\(k\) يجب أولا معرفة الميل \((k)\) وإحداثيات نقطة من النقاط التي تقع على خط هذه الدالة. يمكننا على سبيل المثال استخدام النقطة الأولى المُعطية في المثال أعلاه وهي \((1, 5)\).
الآن يمكننا بكل بساطة إيجاد قيمة \(m\) بتعويض هذه القيّم المعُطية في معادلة الخط المستقيم ومن ثم إيجاد قيمة \(m\) كما يلي:
$$y=kx+m$$
$$5=-\frac{1}{2}\cdot 1+m$$
$$5=-\frac{1}{2}+m$$
$$5+\frac{1}{2}\cdot 1=m$$
$$m=5,5$$
بالتالي معادلة الخط المستقيم هي
$$y=-\frac{1}{2}x+\frac{11}{2}$$
من ميزات استخدام صيغة الميل-\(k\) هي أننا سنحتاج فقط لاستخدام معادلة الخط المستقيم وتعويض القيّم المُعطية ومن ثم إيجاد قيمة \(m\).
صيغة النقطة المعلومة
تماما كما في حالة إيجاد قيمة \(m\) باستخدام صيغة الميل-\(k\) سنحتاج لمعرفة كل من الميل \((k)\) وإحداثيات نقطة من النقاط التي تقع على الخط لإيجاد قيمة \(m\) باستخدام صيغة النقطة المعلومة.
صيغة النقطة المعلومة هي كما يلي
$$y-y_{1}=k(x-x_{1})$$
الآن لإيجاد قيمة \(m\) سنقوم بتعويض قيّم كل من \(y_1\), \(x_1\) و \(k\) المُعطية كما يلي:
$$y-y_{1}=k(x-x_{1})$$
$$y-5=-\frac{1}{2}(x-1)$$
$$y-5=-\frac{1}{2}x+\frac{1}{2}$$
$$y=-\frac{1}{2}x+\frac{11}{2}$$
من ميزات استخدام هذه الصيغة هو عدم ضرورة إيجاد قيمة \(m\) وباستخدامها تحصلنا على معادلة الخط المُستقيم المطلوبة وهي نفس المعادلة التي تحصلنا عليها باستخدام صيغة الميل-\(k\).
فيديوهات الدرس (باللغة السويدية)
معادلة الخط المُستقيم وقيمة الميل \(k\).
قيمة الجزء المقطوع \(m\) للخط المُستقيم.
صيغة الميل-\(k\).
صيغة النقطة المعلومة.
