متعددات الحدود
متعددة أو كثيرة الحدود هي عبارة عن تعبير جبري يمكن استخدامه كنموذج رياضي لوصف العديد من الحالات المختلفة. متعددات الحدود قابلتنا سابقا وفي هذا القسم والأقسام التالية سنتعلم المزيد عنها وعن كيفية استخدام متعددات الحدود في العمليات الحسابية، كما سنتعرف على خصائص متعددات الحدود.
تتكون متعددة الحدود من متغيرات (مثل x, y, z) وثوابت (مثل 2-, 17, 3) ويتم ربطهم معا عن طريق الجمع والطرح والضرب. ويجب أن تكون أُسُس الحدود المتغيرة في متعددة الحدود عبارة عن أعداد صحيحة موجبة. هذا يعني أن التعبيرات الثلاثة التالية تُمثل متعددات حدود:
$$x^2+3x-1$$
$$-3x+2$$
$$2x^4-5x^3-x+7$$
التعبير الجبري الذي يحتوي على حدود متغيرة لها أُسُس غير موجبة أو أعداد غير صحيحة في الأُسُس لا يُعتبر متعدد حدود.
كمثال على ذلك يمكننا وصف حالة سقوط كرة من سطح مبنى عالي
يمكن وصف سرعة الكرة بعد مرور زمن معين بدالة متعددة الحدود التالية:
$$v=9,81\cdot t$$
حيث أن السرعة v تساوي عجلة الجاذبية 9,81 (متر في الثانية) مضروبة في الزمن t (بالثانية، بعد سقوط الكرة)؛ كلما زاد زمن السقوط كلما زادت سرعة الكرة.
في هذا المثال لدينا متعددة حدود في الطرف الأيمن تتكون من حاصل ضرب عدد ثابت (9,81) فـي متغير (الزمن t).
باستخدام دالة متعددة الحدود أعلاه يمكننا حساب سرعة الكرة بعد مرور 3,0 ثواني من بداية سقوط الكرة من أعلى السطح وذلك بتعويض t بالقيمة 3,0:
$$v= 9,81 \cdot 3,0\approx 29 \Large\text{ m/s (متر في الثانية)}$$
درجات متعددات الحدود
غالبا ما يتم وصف متعددة الحدود بذكر درجتها وهي أكبر عدد صحيح موجب في أُسُس الحدود المتغيرة.
في مثال سرعة الكرة أعلاه لدينا متعددة حدود من الدرجة الأولى لأن المتغير في الحد \((9,81t)\) أُسه 1 (بطبيعة الحال \(t\) تعني \(t^1\), أي أن الأُس يساوي 1). متعددة الحدود هذه تحتوي على حد متغير واحد فقط ولكن غالبا ما تحتوي متعددات الحدود على أكثر من حد.
بدأنا هذا القسم بثلاثة أمثلة لمتعددات الحدود، يمكننا الآن الرجوع إليها وتحديد درجة كل منها.
متعددة الحدود:
$$x^2+3x-1$$
هي متعددة حدود من الدرجة الثانية، لأن أكبر أُس في حدودها المتغيرة هو 2 (الحد \(x^2\)).
بينما
$$-3x+2$$
هي متعددة حدود من الدرجة الأولى، لأن أكبر أُس يساوي 1 وهو أُس الحد المتغير الوحيد (\(-3x\)).
وبالمثل متعددة الحدود
$$2x^4-5x^3-x+7$$
هي متعددة حدود من الدرجة الرابعة، لأن لدينا حد متغير أُسه 4 (الحد \(2x^4\)).
الحدود المتغيرة ذات الدرجات المختلفة
متعددات الحدود تنطبق عليها نفس القواعد الحسابية للأعداد العادية. لكن عندما نتعامل مع متعددات الحدود علينا أن نتذكر أن الحدود المتغيرة ذات الدرجات المختلفة لا يمكن جمعها مع بعضها البعض. على سبيل المثال هناك اختلاف كبير بين الحدين المتغيرين \(x^2\) و \(x^3\) لأن
$$x^{2}=x\cdot x$$
$$x^{3}=x\cdot x\cdot x$$
وهذا يعني أن \(x^3\) أكبر من \(x^2\) بــ \(x\) مرة.
فإذا كنا لدينا متعددة حدود تتكون من حدود متغيرة ذات درجات مختلفة يجب كتابة هذه الحدود بشكل منفصل ومرتبة حسب درجاتها.
في المثال التالي سنرى كيف يمكننا ترتيب الحدود المتغيرة ذات الدرجات المختلفة
$$x^{3}+2x+3x^{3}-x=(x^{3}+3x^{3})+(2x-x)=4x^{3}+x$$
(في العملية الحسابية أعلاه تم استخدام الأقواس فقط لتسهيل عملية تجميع الحدود المتغيرة ذات الدرجة المتشابهة).
بالتالي قمنا بجمع وطرح الحدود المتغيرة ذات الدرجة المتشابهة. وهكذا يمكننا تبسيط متعددات الحدود.
ضرب متعددات الحدود
في عمليات ضرب متعددات الحدود من المهم جدا أن نتذكر ضرب جميع حدود المتعددة المضروبة فـي جميع حدود المتعددة المضروب فيها.
إذا نظرنا إلى مثال عملية ضرب متعددات الحدود التالي
$$2x\cdot (4+3x)$$
بالتالي يمكننا حساب حاصل الضرب هذا بتطبيق خاصية التوزيع التي قابلناها عند دراستنا لخصائص الأعداد الصحيحة.
يمكننا تطبيق قانون التوزيع على عامل الضرب a وحدود عامل الضرب الثاني b وc وفقا للعلاقة التالية:
$$a\cdot (b+c)=a\cdot b+a\cdot c$$
إذا قارنا هذه العلاقة بحاصل الضرب أعلاه يمكن أن نتعامل مع عوامله كما يلي: \(a = 2x\), \(b = 4\) و \(c = 3x\).
بالتالي سنحسب حاصل جمع \((2x \cdot 4)\) زائدا \((2x \cdot 3x)\). أي سنقوم بضرب الحد \(2x\) فـي جميع حدود متعددة الحدود داخل القوسين \((4 + 3x)\).
لذا سنحصل على:
$${\color{Blue} {2x}}\cdot ({\color{Red} {4+3x}})=$$
$${\color{Blue} {2x}}\cdot{\color{Red} {4}}+{\color{Blue} {2x}}\cdot {\color{Red} {3x}}=$$
$$8x+6x^{2}$$
أيضا يمكننا ملاحظة أن حاصل ضرب متعددتي حدود من الدرجة الأولى هو عبارة عن متعددة حدود من الدرجة الثانية.
عند ضرب متعددات الحدود يجب أن ننتبه لعلامة الحد المضروب فيما بداخل القوس، فيجب أن نضع لها اعتبار فقد تكون موجب أو سالب وهي العلامة الواقعة شماله مباشرة.
فإذا كان هناك علامة سالب أمام القوسين سيتم عكس العلامات داخل القوسين عند عملية الضرب.
لنرى ذلك في المثال التالي
$$3-{\color{Blue} {2x}}\cdot ({\color{Red} {4+3x}})=$$
$$3-({\color{Blue}{ 2x}}\cdot {\color{Red} 4}+{\color{Blue} {2x}}\cdot {\color{Red} {3x}})=$$
$$3-(8x+6x^{2})$$
$$3-8x-6x^{2}$$
إذا أردنا ضرب قوسين معا فيجب ضرب كل حد من حدود القوسين الأوليّن فـي جميع حدود القوسين الآخريّن. لنرى ذلك في حالة ضرب متعددتي حدود من الدرجة الأولي وكل منهما تحتوي على حد متغير وحد ثابت، فيما يلي كيفية ضربهما:
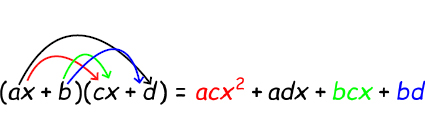
وفيما يلي مثال على ذلك، وفيه لدينا متعددتي حدود كل منهما تحتوي على المتغيرين \(x\) و\(y\)، ولكن طريقة حساب حاصل ضربهما هي نفس الطريقة أعلاه.
$$({\color{Red} {5x}}+2y)\cdot ({\color{Green} {3x}}+{\color{Blue} {4y}})=$$
$$={\color{Red} {5x}}\cdot {\color{Green}{ 3x}}+{\color{Red} {5x}}\cdot {\color{Blue} {4y}}+2y\cdot {\color{Green} {3x}}+2y\cdot {\color{Blue} {4y}}=$$
$$=15x^{2}+20xy+6xy+8y^{2}=$$
$$=15x^{2}+26xy+8y^{2}$$
عملية ضرب جميع حدود متعددة الحدود الأولى في جميع حدود متعددة الحدود الثانية يمكننا توضيحها في الشكل أدناه، حيث كل متعددة حدود تُمثيل أحد أضلاع المستطيل الكبير وحاصل ضربهما يُمثل مساحته:
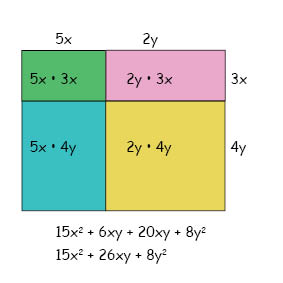
أي أن حاصل ضرب أضلاع المستطيل هو عبارة عن مساحة المستطيل. المساحة الكلية للمستطيل هي عبارة عن مجموع مساحات المستطيلات الصغيرة (المظللة باللون الأخضر، الوردي، الأزرق والأصفر)، بمعني أن المساحات الجزئية تُشكل معا المساحة الكلية (حاصل ضرب متعددتي الحدود).
في هذا القسم من بين أمور أخرى ناقشنا كيفية ضرب متعددتي الحدود. هناك بعض الحالات الخاصة المفيدة جدا في عمليات ضرب متعددات الحدود وينبغي معرفتها، هذه الحالات الخاصة سنناقشها الآن في القسمين القادمين وهما قواعد التربيع و قاعدة ضرب المترافقين
فيديوهات الدرس (باللغة السويدية)
في هذا الفديو سنشرح مفهوم متعددة حدود.
في الفديوهات التاليه سنشرح عملية ضرب متعددة حدود (ذات حدين.
في هذا الفيديو سنشرح كيف يمكننا استخدام متعددة الحدود للتعبير عن مساحة المستطيل.
