صيغة المسافة
في هذا القسم سنتعلم احدى تطبيقات نظرية فيثاغورس وهي ما تُسمى بصيغة المسافة.
يمكن استخدام صيغة المسافة لحساب المسافة بين نقطتين على نظام الإحداثيات وهي تطبيق من تطبيقات نظرية فيثاغورث التي تُستخدم بصورة أساسية في تحديد العلاقة بين أطوال أضلاع المثلث القائم الزاوية.
لنرسم نقطتين على نظام إحداثيات ونحاول إيجاد طول المسافة بين هاتين النقطتين.
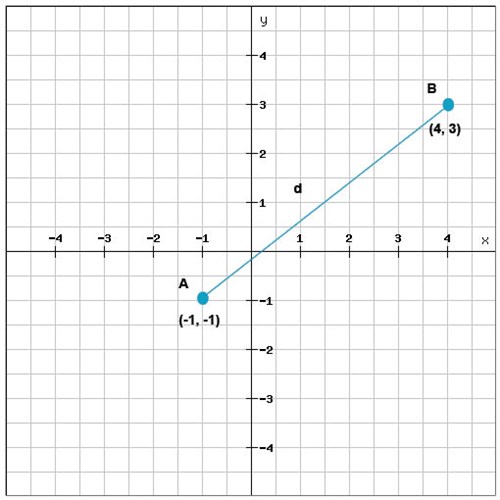
يمكننا تكوين مثلث قائم الزاوية من هذه النقاط وذلك برسم خطين، خط موازي لمحور \(x\) وخط آخر موازي لمحور \(y\), بحيث تكون المسافة بين النقطتين A و B (المشار إليها بـ d في الصورة) هي وتر هذا المثلث.
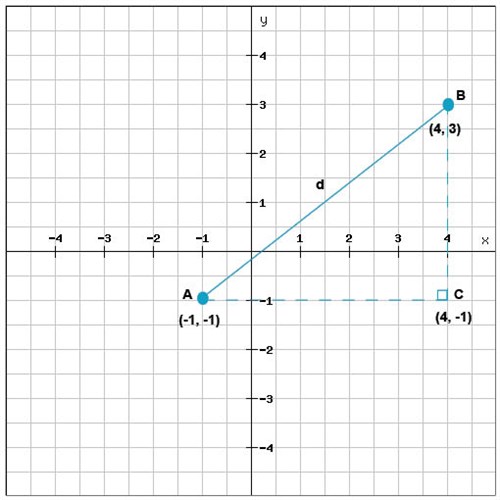
ومن ثم يمكننا حساب طول الضلعين المتعامدين AC و BC
$$AC=x_{C}-x_{A}=4-(-1)=5\, \textsf{وحدات طولية}$$
$$BC=y_{B}-y_{C}=3-(-1)=4\, \textsf{وحدات طولية}$$
يمكننا حساب طول المسافة \(d\) باستخدام نظرية فيثاغورث كما يلي:
$$a^{2}+b^{2}=c^{2}$$
حيث أن \(a\) و \(b\) هما الضلعان المتعادان في المثلث و \(c\) هو الوتر.
في هذا المثال يُرمز للموتر بالحرف \(d\) والضلعان المتعامدان هما \(AC\) و \(BC\) بالتالي سنحصل على المسافة \(d\) كما يلي:
$$ d^2=(AC)^2+(BC)^2=5^2+4^2=25+16=41$$
$$d=\sqrt{41}\approx6,4\, \textsf{وحدات طولية}$$
إذن المسافة بين النقطة A والنقطة B هي حوالي 6.4 وحدات طولية.
بصورة عامة صيغة حساب المسافة بين أي نقطتين على نظام الإحداثيات هي:
$$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
حيث أن \(d\) هي المسافة بين النقطتين, \(x_1\) و \(y _1\) هما إحداثيات النقطة الأولى و \(x_2\) و \(y _2\) هما إحداثيات النقطة الثانية.
فيديوهات الدرس (باللغة السويدية)
في هذا الفيديو سنشرح كيف يمكننا حساب المسافة بين نقطتين على نظام الإحداثيات بإستخدام صيغة المسافة.
مثال آخر على استخدام صيغة المسافة.
