نظرية الزاوية المحيطية
هذا القسم يدخل في مقرر كل من رياضيات 2b ورياضيات 2c.
قبل الدخول في شرح هذه النظرية سنبدأ بدراسة بعض المفاهيم التمهيدية الهامة.
تعريفات
نبدأ من الدائرة الموضحة في الشكل أدناه.
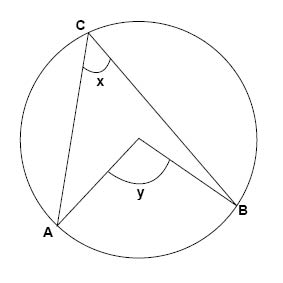
في هذا الشكل أعلاه لدينا نقطة في منتصف الدائرة تُسمى بمركز الدائرة. ولدينا أيضا النقطتين A و B الواقعتين على محيط الدائرة، أي على بُعد مسافة نصف القطر من مركز الدائرة. ويشكل هاتان النقطتان القوس AB. لدينا أيضا نقطة ثالثة C وتقع أيضا على محيط الدائرة. المسافة بين أي نقطتان يقعان على محيط الدائرة تُسمى بالوتر كالمسافات AC و BC في الشكل.
بالإضافة إلى ذلك لدينا زاويتين مهمتين: الزاوية المركزية y الناشئة على القوس AB وزاوية المحيط x عند النقطة C وهي الزاوية المحصورة بين الوترين CA و CB كما في الشكل أعلاه.
نظرية الزاوية المحيطية
تنص نظرية الزاوية المحيطية على أن زاوية القوس AB المركزية (y) تساوي ضعف الزاوية (x) الواقعة على نفس القوس AB, أي أن
$$y=2x$$
نظريات مُستنتجة
من نظرية الزاوية المحيطية يمكننا الحصول على النظريات التالية:
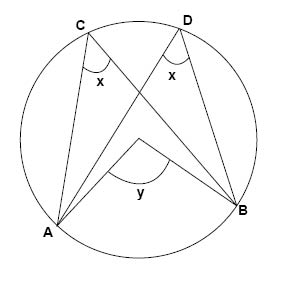
جميع الزوايا المحيطية الناشئة على نفس القوس متساوية وذلك لأن نظرية الزاوية المحيطية تنص على أن الزاوية المحيطية تساوي نصف مقدار الزاوية المركزية الناشئة على نفس القوس وبما أن جميع الزوايا ناشئة على نفس القوس سيكون مقدار كل منها يساوي نصف مقدار الزاوية المركزية.
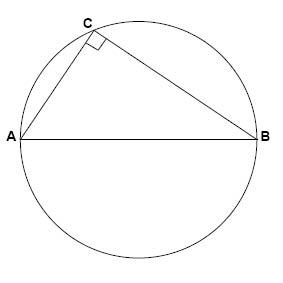
الزاوية المحيطية للقوس النصف دائري تساوي \(90°\) وذلك لأن نصف الدورة يساوي \(180°\). وتسمى هذه النظرية بنظرية طالس.
إذا رسمنا شكل رباعي داخل دائرة سيكون مجموع الزوايا المتقابلة دائما \(180°\).
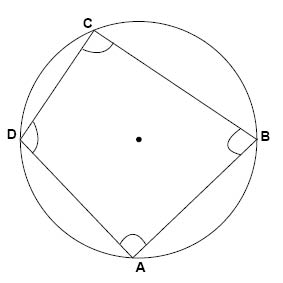
$$\measuredangle A+\measuredangle C=180^{\circ}$$
$$\measuredangle B+\measuredangle D=180^{\circ}$$
إثبات صحة نظرية الزاوية المحيطية
فيما يلي برهان الزاوية المحيطية.
لإثبات صحة نظرة الزاوية المحيطية سنبدأ برسم قطر يمر برأسي الزاويتين. بحيث يقوم هذا القطر بتقسيم الزاوية x الى زاويتين \(x_1\) و \(x_2\) والزاوية y الى زاويتين \(y_1\) و \(y_2\).
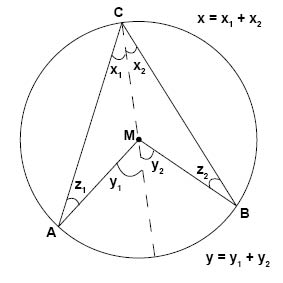
الزاويتان \(y_1\) و \(y_2\) تمثلان زاويتان خارجيتان لكل من \(\triangle AMC\) و \(\triangle BMC\)، وقانون الزاوية الخارجية ينص على أن
$$y_{1}=x_{1}+z_{1}\;\;و\;\;y_{2}=x_{2}+z_{2}$$
وبما أن المثلث ACM والمثلث BCM مثلثان متساويان الساقان (الأضلاع CM, AM و BM جميعها تساوي نصف قطر الدائرة)، بالتالي
$$x_{1}=z_{1}\;\;و\;\;x_{2}=z_{2}$$
وهذا يعني أن
$$y_{1}=x_{1}+x_{1}=2x_{1}\;\;och\;\;y_{2}=x_{2}+x_{2}=2x_{2}$$
$$y_{1}+y_{2}=2x_{1}+2x_{2}=2(x_{1}+x_{2})$$
$$y=2x$$
وهو المطلوب إثباته.
فيديوهات الدرس (باللغة السويدية)
نستعرض في هذا الفلم نظرية الزاوية المحيطية.
حالة من ثلاث حالات ممكنة لإثبات صحة نظرية الزاوية المحيطية.
النظريات التي يمكن استنتاجها من نظرية الزاويه المحيطيه.
