الأرباع ومُخطط الصندوق
في قسم المقاييس الموضعية السابق اخذنا مثال وجبة عشاء أسرة Mattecentrum وكانت أعمار الذين حضروا هذا العشاء كما يلي
$$1,\, 4,\, 3,\, 15,\, 72,\, 41,\, 30,\, 27,\, 72,\, 8,\, 42,\, 36,\, 33,\, 46,\, 44$$
ماتياس كان واحد من الذين لم يحضروا وجبة عشاء هذه الأسرة وبدلا من ذلك كان في وجبة عشاء مع عدد من أصدقائه. أعمار الخمسة عشر شخص الذين تناول معهم ماتياس وجبة العشاء كانت كما يلي:
$$30,\, 31,\, 33,\, 34,\, 35,\, 34,\, 28,\, 34,\, 33,\, 34,\, 36,\, 35,\, 32,\, 31,\, 32$$
لنقارن المقاييس الموضعية لأعمار أفراد هاتين المجموعتين. لاحظنا أن قيمتي المتوسط والوسيط لأفراد وجبة عشاء الأسرة كانتا
المتوسط هو
سنة \(medel=31,6\)
والوسيط هو
سنة \(median=33 \)
أما بالنسبة للأشخاص الذين حضورا وجبة عشاء الأصدقاء، فكانت هذه المقاييس الموضعية كما يلي:
المتوسط هو
سنة \(medel=32,8\)
والوسيط هو
سنة \(median=33\)
إذا نظرنا إلى هذه المقاييس الموضعية فقط فلا يبدو أن هنالك فرق كبير بين الأعمار في الحالتين، أما إذا قارنا قيمتي المتوسطين فقد يبدو أن أعمار مجموعة الأصدقاء أكبر من أعمار أفراد الأسرة. ومع ذلك نلاحظ أن هنالك فرق كبير في كيفية توزيع (تشتُت) أعمار المجموعتين – أي أن الفرق بين مجموعة من أعمار أفراد الأسرة أكبر من الفرق بين أعمار الأصدقاء.
ولمثل هذه الأسباب تم تقديم مقاييس تشتُت مختلفة للمقارنة بين مجموعتين أو أكثر من القراءات الإحصائية. عن طريق مقاييس التشتُت يمكننا الحصول على صورة أكثر دِقة عن مجموعة من القراءات الإحصائية المختلفة وكيفية تشتُت عينات (قيّم) هذه القراءات. في هذا القسم سندرس مفاهيم كل من عرض التغيّر، الأرباع (أو الرُبيعات) ومُخطط الصندوق وذلك لكي نستطيع استيعاب مفهوم الانحراف المعياري في القسم القادم وهو عبارة عن مقياس مدى انحراف القيّم عن القيمة المتوسطة لهذه القيّم (القراءات).
عرض التغيّر (Variationsbredd)
عرض التغيّر هو مقياس بسيط لمدى تشتُت قيّم القراءات الإحصائية، وهو عبارة عن الفرق (الاختلاف) بين أكبر قيمة وأصغر قيمة في مجموعة من القيّم.
في مثال وجبة عشاء الأسرة يمكننا الحصول على عرض التغيّر في أعمار الأفراد بطرح أصغر عمر (1 سنة) من أكبر عمر (72 سنة)
بمعنى أن عرض التغيّر هو
سنة \(72-1=71\)
بنفس الطريقة يمكننا حساب عرض التغيّر في أعمار مجموعة الأصدقاء، حيث أن أكبر عمر هو 36 سنة وأصغر عمر هو 28 سنة. وفي هذه الحالة سيكون عرض التغيّر
سنة \(36-28=8\)
كما نلاحظ حصلنا على قيّم مختلفة تماما لعرض التغير في المجموعتين، تعتمد قيمة عرض التغيّر على مقدار تشتُت القيّم، فهو أكبر بكثير في حالة أفراد الأسرة.
بالتالي فإن عملية حساب عرض التغيّر عملية سهله جدا ولكن من سلبيات هذا المقياس عدم وضع كل قيّم المجموعة في الاعتبار وانما يتم حسابه بأخذ أكبر قيمة وأصغر قيمة فقط. لذلك يمكن استخدام مقاييس تشتُت أخرى للحصول على صورة أفضل للتشتُت.
الأرباع أو الرُبيعات (Kvartiler)
هناك طريقة أفضل لوصف التشتُت حول الوسيط وهي تقسيم قيّم القراءات إلى أرباع (رُبيعيات). يمكننا الحصول على الأرباع بتقسيم مجموعة القيّم بعد ترتيبها حسب الحجم (أي من الأصغر الى الأكبر) الى أربعة مجموعات متساوية.
هناك خمسة قيّم مهمة يجب مراعاتها عند تقسيم مجموعة من القيّم إلى أرباع:
أقصى قيمتين في طرفي القراءات وهما أكبر قيمة وأقل قيمة وهما القيمتان اللذان يُستخدمان في حساب عرض التغيُر كما في القسم السابق.
أيضا سنحتاج الى معرفة الوسيط وهو القيمة الواقعة في منتصف القيّم بعد ترتيبها، بمعنى أنه سيُقَسـِم مجموعة القيّم الى مجموعتين متساويين بعد الترتيب.
آخر قيمتين يجب معرفتهما هما:
- القيمة الواقعة عند نهاية الرُبع الأدنى (الأول) وهي التي تُقَسِم النصف الأول (الـ \(50\%\) الأولى من القيّم) إلى جزأين متساويين.
- القيمة الواقعة عند بداية الرُبع الأعلى (الرابع) وهي التي تُقَسِم النصف الثاني (الـ \(50\%\) الثانية من القيّم) إلى جزأين متساويين. وهذا يعني أن القيّم التي تُمثل \(25\%\) من القراءات ستكون أقل من قيمة نهاية الرُبع الأدنى والقيّم التي تُمثل الــ \(75\%\) من القراءات ستكون أقل من قيمة بداية الرُبع الرابع.
غالبا ما يُرمز لنهاية الرُبع الأدنى بــ Q1 والوسيط بــ Q2, وبداية الرُبع الأعلى بــ Q3.
الشكل التالي يوضح كيفية ارتباط هذه القيّم الخمس بقيّم القراءات الأخرى.
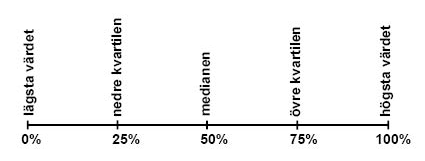
معاني الكلمات السويدية:
| اللغة السويدية | اللغة العربية |
| lägsta värdet | أقل قيمة |
| nedre kvartilen | الرُبع الأدنى |
| medianen | الوسيط |
| övre kvartilen | الرُبع الأعلى |
| högsta värdet | أعلى قيمة |
الآن بعد تعريف مفهوم هذه القيّم الخمس يمكننا حسابها في مثالي وجبة العشاء السابق
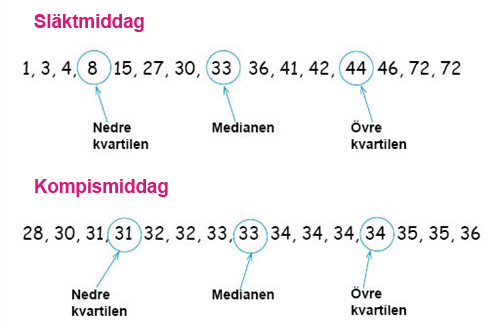
Släktmiddag تعني عشاء الأسرة و Kompismiddag تعني عشاء الأصدقاء.
الفرق بين قيمتي Q1 و Q3 يُسمى بالمسافة الرُبيعية وهي تُعادل عرض تغيّر الـ \(50\%\) من القيّم الواقعة في منتصف مجموعة القيّم. وهذا يعني أن المسافة الرُبيعية هي عبارة عن مقياس لمقدار التشتُت حول الوسيط.
من هذا التعريف يمكننا حساب المسافة الرُبيعية لأعمار المشاركين في وجبة عشاء الأسرة كما يلي
سنة \(44-8= 36\)
بنفس الطريقة يمكننا حساب المسافة الرُبيعية لأعمار المشاركين في وجبة عشاء الأصدقاء على النحو التالي
سنة \(34-31=3\)
مخطط الصندوق
باستخدام مفاهيم هذه الأرباع المذكورة أعلاه يمكننا توضيح معنى التشتُت حول الوسيط باستخدام مخطط الصندوق.
يتم رسم مخطط الصندوق على خط الأعداد وهو عبارة عن صندوق في شكل مستطيل بدايته عند النقطة Q1 ونهايته عند النقطة Q3 ويتم تحديد الوسيط بخط عمودي داخل الصندوق (عند النقطة Q2). أيضا لدينا خط أفقي ممتد من طرف الصندوق الأيسر الى القيمة الصغرى ومن طرف الصندوق الأيمن الى القيمة الكبرى.
فيما يلي لدينا رسم توضيحي لمخطط صندوق لمجموعة من القيّم، تتراوح هذه القيّم ما بين 1 (أصغر قيمة) إلى 21 (أعلى قيمة). في هذا المثال قيمة الوسيط هي 11, قيمة الرُبع الأدنى هي 6 وقيمة الرُبع الأعلى هي 16.
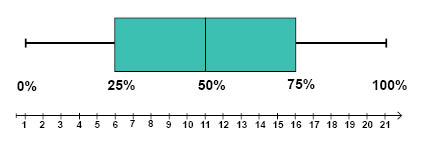
بنفس الطريقة يمكننا توضيح قيّم قراءات دراستنا الإحصائية لأعمار المشاركين في وجبة عشاء الأسرة والأصدقاء باستخدام مخطط الصندوق كما يلي.
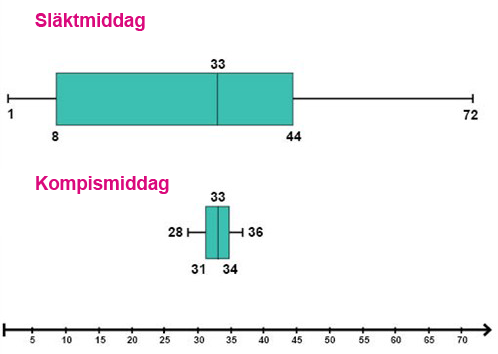
الآن نلاحظ الفرق الواضح في تشتُت أعمار الأسرة وتشتُت أعمار الأصدقاء بالرغم من أن الوسيط هو 33 سنة للحالتين.
المئويات (Percentiler)
بنفس الطريقة كما يمكننا تقسيم أي مجموعة من القراءات الإحصائية إلى أرباع (رُبيعيات)، يمكننا أيضا تقسيم المجموعات الكبيرة من القراءات الإحصائية إلى عدد من الأجزاء المئوية وفي هذه الحالة تُسمى الأجزاء بالمئويات.
بعض المئويات تُسمى بالأرباع (الرُبيعات). على سبيل المثال الربيع الأدنى Q1 يطابق المئوية الـ 25 ويُرمز له بــ P25 (ما يعني أن قيّم هذا الرُبع ستكون أقل من هذه القيمة). وبنفس المفهوم يمكن تسمية الوسيط بالرمز P50 والربيع الأعلى Q3 بالرمز P75.
وبما أن لدينا عدد قراءات قليل جدا في حالتي هذا العشاء (15 قيمة في كل حالة)، فإن استخدام الرُبيعيات أنسب من المئويات. أما إذا كان لدينا مجموعة تتكون من عدد كبير من القراءات الإحصائية، على سبيل المثال إذا قمنا بدراسة إحصائية لأعمار ألف شخص فسيكون استخدام المئويات هو الأنسب في هذه الحالة.
في القسم القادم سنواصل في دراسة كيفية تحديد تشتُت القراءات الإحصائية باستخدام ما يُسمى بالانحراف المعياري.
فيديوهات الدرس (باللغة السويدية)
كيفية بناء ورسم مخطط الصندوق.
هنا سنشرح مفهوم كل من التشتُت, عرض التغيّر والمسافة الرُبيعية.
مثال آخر على كيفية رسم مخطط الصندوق.
استخدام الآلة الحاسبة لرسم مخطط الصندوق
هنا تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس المثال على الآلة الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من الماركات الأخرى تحتوي على نفس الوظائف تقريباً.
