معادلات الدرجة الثانية
في الباب السابق تحدثنا عن متعددات الحدود وخلصنا إلى أن درجة متعددة الحدود هي عبارة عن أكبر أُس (قوة) في متغيراتها. مثلا عندما تكون درجة متعددة الحدود 2 تُسمى بمتعددة حدود من الدرجة الثانية.
المعادلة التي يتكون أحد طرفيها من متعددة حدود من الدرجة الثانية وطرفها الآخر يساوي صفر تُسمى بمعادلة من الدرجة الثانية. هذا النوع من المعادلات مهم جدا وسنقابله في العديد من السياقات المختلفة ولذلك سنركز على دراسة معادلات الدرجة الثانية في هذا القسم والأقسام التالية من هذا الباب.
متعددات الحدود ذات الدرجة الثانية
بصورة عامة يمكننا كتابة متعددة حدود من الدرجة الثانية كما يلي:
$$ax^{2}+bx+c$$
حيث a و b و c ثوابت و \(a \neq 0\) (إذا كان a = 0 فإن الحد الذي يحتوي على \(x^2\) سيساوي صفر وفي هذه الحالة ستختفي الدرجة 2 أي أن متعددة الحدود ليست من الدرجة الثانية، ومع ذلك لا مانع من أن تكون قيمة كل من b أو c (أو الإثنين معا) تساوي صفر).
مثال على متعددة حدود من الدرجة الثانية
$$x^{2}+3x+1$$
حيث أن \(x^2\) هو الحد المتغير الذي يحتوي على أكبر أُس ولذلك فهو الحد الذي يُحدد درجة المتعددة. بمقارنة هذا المثال مع الصورة العامة أعلاه ستكون قيّم الثوابت هي (\(a = 1\) و \(b = 3\) و \(c = 1\)) ولكن عندما يكون معامل \(x\) هو عبارة عن واحد صحيح (1) عادة ما لا يُكتب.
دوال الدرجة الثانية
دوال الدرجة الثانية هي الدوال التي يمكن كتابتها على النحو التالي
$$f(x)=ax^{2}+bx+c$$
حيث أن a و b و c ثوابت و \(a \neq 0\). وهي عبارة عن دالة حيث أن تعبير الدالة \(f(x)\) يتكون من متعددة حدود من الدرجة الثانية.
يمكن استخدام مثال متعددة الحدود أعلاه وكتابته في صورة دالة من الدرجة الثانية كما يلي
$$f(x)=x^{2}+3x+1$$
معادلات الدرجة الثانية
إذا كان لدينا معادلة في الصيغة \((f (x) = 0)\), حيث أن \(f (x)\) عبارة عن دالة من الدرجة الثانية وفقا للصيغة العامة أعلاه, فيُسمى هذا النوع من المعادلات بمعادلات الدرجة الثانية.
أي أن معادلات الدرجة الثانية يمكن كتابتها كما يلي
$$ax^{2}+bx+c=0$$
حيث أن a و b و c ثوابت و \(a \neq 0\).
ليست كل معادلات الدرجة الثانية التي ستقابلنا مكتوبة بالصيغة أعلاه ولكن جميع معادلات الدرجة الثانية التي تكون مكتوبة بصيغة أخرى يمكن إعادة كتابتها لهذا الصيغة. على سبيل المثال قد يكون لدينا حد ثابت في الطرف الأيمن بدلا من الصفر، في مثل هذه الحالات سنطرح أولا الحد الثابت من كلا الطرفين لكي يكون لدينا صفر في الطرف الأيمن. العمليات الحسابية التي يمكن إجراءها لإعادة كتابة معادلات الدرجة الثانية للصيغة المطلوبة تختلف من حالة إلى أخرى حسب الصيغة الواردة.
من مثال متعددة الحدود أعلاه يمكننا كتابة معادلة الدرجة الثانية كما يلي
$$x^{2}+3x+1=0$$
حل معادلة الدرجة الثانية يعني إيجاد قيمة أو قيّم المتغير المُستخدم بحيث تكون \((f (x) = 0)\) أي أن قيمة متعددة الحدود تساوي صفر عندما نعوض قيمة المتغير.
سنرى الآن العلاقة بين معادلات الدرجة الثانية والدوال المقابلة لها وكيف يمكننا استخدام ذلك لحل معادلات الدرجة الثانية وإيجاد قيّم المتغيرات المطلوبة عند دارسة دوال الدرجة الثانية.
النقاط القصوى لدوال الدرجة الثانية
أبسط متعددة حدود من الدرجة الثانية هي
$$x^{2}$$
بالمقارنة مع الصورة العامة لمتعددة الحدود نلاحظ أن قيّم الثوابت في هذه المتعددة هي \((a = 1)\) و \((b = 0)\) و \((c = 0)\) وعادة ما لا نكتب مثل هذه القيّم, أما إذا كتبناها سنحصل على ما يلي:
$$ 1\cdot x^2+0\cdot x+0$$
دالة الدرجة الثانية المقابلة هي
$$f(x)=x^{2}$$
إذا رسمنا هذه الدالة بيانيا على نظام الإحداثيات فستكون كما يلي:
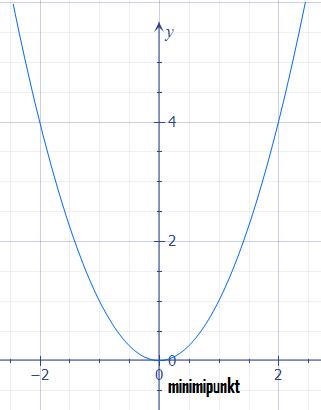
الدالة التي يكون مخططها البياني كما في الشكل أعلاه تُسمى بالقطع المكافئ (parabel) وهي دالة غير خطية.
ستكون قيمة الدالة الصغرى عند \((x = 0)\). النقطة التي تأخذ فيها الدالة قيمتها الصغرى تُسمى بالنقطة الصغرى. عندما يكون لدينا دالة من الدرجة الثانية وفيها معامل الحد \(x^2\) عبارة عن عدد موجب فعادة ما يكون للدالة نقطة صغرى عند إحدى قيّم \(x\).
إذا نظرنا بدلا من ذلك إلى دالة من الدرجة الثانية حيث أن معامل الحد \(x^2\) عبارة عن عدد سالب مثل الدالة التالية
$$f(x)=-x^{2}$$
ورسمناها بيانيا على نظام الإحداثيات فسنحصل على الشكل التالي:
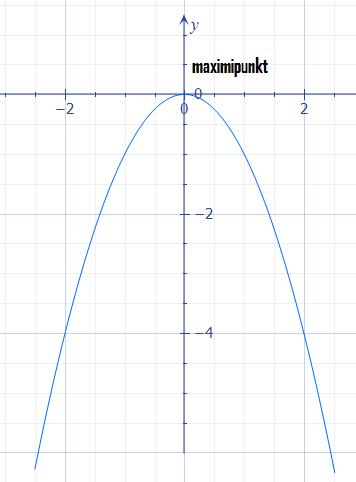
فإن هذه الدالة لها قيمة عظمى عندما يكون \((x = 0)\) والنقطة التي تأخذ فيها الدالة قيمتها العظمى تُسمى بالنقطة العظمى. دوال الدرجة الثانية التي يكون فيها معامل الحد \(x^2\) عبارة عن عدد سالب عادة ما يكون لها نقطة عظمى عند إحدى قيّم \(x\).
تُسمى النقاط العظمى والصغرى بالنقاط القصوى. إذا أردنا إيجاد النقاط القصوى لدالة ما فهذا يعني أننا نبحث عن النقاط العظمى أو الصغرى أو كلاهما.
في العديد من السياقات غالبا ما نهتم بإيجاد قيمة الدالة العظمى أو قيمها الصغرى.
هناك قاعدة بسيطة يمكن استخدامها لتحديد ما إذا كانت دالة الدرجة الثانية لها نقطة صغرى أم لها نقطة عظمى. عندما يكون معامل الحد \(x^2\) عبارة عن عدد موجب فسيكون شكل مخطط الدالة البياني كالفم السعيد (إيجابي)، وبالتالي سيكون لها نقطة صغرى. بنفس الطريقة عندما يكون معامل الحد \(x^2\) عبارة عن عدد سالب فسيكون شكل مخطط الدالة البياني كالفم الحزين (سلبي) لذا سيكون لمثل هذه الدوال نقطة عظمى.
نقاط انعدام الدالة
إذا رسمنا الدالة التالية بيانيا
$$f(x)=x^{2}+3x-4$$
فسيكون شكلها تقريبا كما يلي:
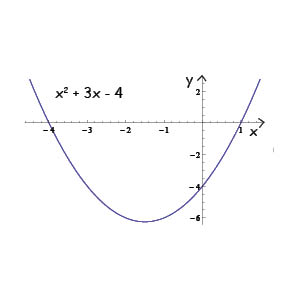
نلاحظ أن المنحنى يتقاطع مع محور \(x\) في نقطتين: حيث أن في احدى النقطتين \((x = -4)\) وفي النقطة الأخرى \((x=1)\)
هاتان القيمتان لـ \(x\) يُسميان بنقاط انعدام الدالة (النقاط التي تساوي عندها الدالة صفر) ويُمثلان حلول أو جذور معادلة الدرجة الثانية المقابلة:
$$x^{2}+3x-4=0$$
كما لخصنا في بداية هذا القسم أن معادلة الدرجة الثانية هي عبارة عن معادلة يمكن كتابتها في الصورة \((f (x) = 0)\) حيث أن \(f (x)\) هي دالة من الدرجة الثانية. وحلها هو قيمة أو قيّم المتغير التي تجعل المتعددة تساوي صفر.
ما قمنا به هنا هو ببساطة أننا قمنا برسم دالة من الدرجة الثانية بيانيا ومن ثم بحثنا عن قيّم \(x\) التي تجعل \((f (x) = 0)\) أي قيّم \(x\) التي تجعل طرفي المعادلة يساوي صفر.
حل معادلات الدرجة الثانية برسمها بيانيا على نظام الإحداثيات وقراءة النقاط التي تنعدم فيها الدالة يُسمى بالحل البياني.
حل معادلة الدرجة الثانية الذي يقع على خط الأعداد الحقيقي يُسمى بالحل الحقيقي. فقيمتي \(x\) اللتان قرأناهما من نظام الإحداثيات في المثال أعلاه \((x = -4)\) و \((x = 1)\) هما حلان حقيقيان.
عدد الحلول
في المثال أعلاه نلاحظ أن معادلة الدرجة الثانية
$$x^{2}+3x-4=0$$
لها حلين حقيقيين وذلك لأن منحنى الدالة يتقاطع مع محور \(x\) مرتين (عندما تكون \(x = -4\) وعندما تكون \(x = 1\)).
أما معادلة الدرجة الثانية البسيطة
$$x^{2}=0$$
فلها حل حقيقي واحد فقط لأن منحنى الدالة \(f(x)=x^2\) يتقاطع مع محور \(x\) مرة واحدة فقط (عند النقطة الصغرى أي عندما تكون \(x = 0\)):

أما إذا كان لدينا دالة من الدرجة الثانية وفقا للصيغة التالية
$$f(x)=x^{2}+2x+2$$
فسيكون لها مخطط بياني كما يلي:
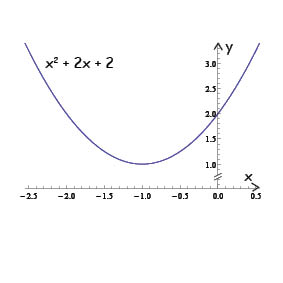
نلاحظ أن منحنى هذه الدالة لا يتقاطع مع محور \(x\) ولها قيمة صغرى عند النقطة التي يكون فيها \((x = -1)\) وهذا المنحنى سوف لن ينزل أسفل هذه النقطة في اتجاه \(y\) أي أن هذه النقطة هي أدنى حد له.
فإذا حاولنا حل هذه المعادلة بيانيا
$$x^{2}+2x+2=0$$
فمن الشكل سنلاحظ أن هذه الدالة ليس لها نقاط انعدام وهذا يعني أن المعادلة ليس لها حلول حقيقية. وبما أن المعادلة ليس لها حلول حقيقية فهذا يعني عدم وجود قيّم حقيقية يمكن تعويضها عن المتغير لكي يساوي طرفي المعادلة صفر.
ما توصلنا إليه الآن هو ثلاث حالات مختلفة من الحالات التي يمكن أن تقابلنا عندما نحاول حل معادلات الدرجة الثانية:
فالمعادلة إما أن يكون لها حلان حقيقيان أو حل حقيقي واحد أو ليس لها حل حقيقي. فهذه الحالات الثلاث يقابلها أن دالة الدرجة الثانية المقابلة قد تحتوي على نقطتي انعدام أو نقطة انعدام واحدة فقط أو لا تحتوي على أي نقاط انعدام.
خط التماثل
دوال الدرجة الثانية عادة ما تكون متماثلة حول خط تماثل معين، أي أن منحنى الدالة على يسار خط التماثل هو عبارة صورة مرآة لمنحنى الدالة على يمين خط التماثل.
مثال على ذلك هو دالة الدرجة الثانية \((y (x) = x²)\) التي تم رسمها بيانيا أعلاه وهي دالة متماثلة حول محور \(y\) (أي عندما يكون \(x = 0\)).
خط تماثل دوال الدرجة الثانية عادة ما يكون عموديا وموازيا لمحور \(y\) والنقاط القصوى لدوال الدرجة الثانية تقع دائما على خط التماثل وتقع دائما في منتصف المسافة بين نقطتي انعدام الدالة وهي خاصية مفيدة، بحيث أنه إذا علمنا نقاط انعدام الدالة يمكننا حساب ومعرفة النقاط التي سيمر بها خط التماثل، والذي بدوره يمكننا تحديد النقطة القصوى للدالة.
بحساب متوسط نقاط الانعدام يمكننا الحصول على خط التماثل. الآن سنستخدم هذه الخاصية لتحديد القيمة القصوى للدالة التي قابلناها سابقا في هذا القسم وهي بالتحديد الدالة
$$f(x)=x^{2}+3x-4$$
كما رأينا سابقا أن هذه الدالة تحتوي على نقطتي انعدام فيها \((x = -4)\) و \((x = 1)\):

بما أننا نعلم أن خط التماثل يجب أن يقع بين هاتان النقطتان (نقطتا الانعدام) فإن قيمة \(x\) لخط التماثل يمكن حسابها كما يلي
$$\frac{(-4)+1}{2}=\frac{-3}{2}=-1,5$$
وبما أن خط التماثل هو عبارة عن خط عمودي ويمكن تحديده بقيمة \(x\) هذه، أي أن \((x = -1.5)\) على طول هذا الخط, فإن النقطة القصوى للدالة ستقع في مكان ما على طول هذا الخط العمودي.
وإذا رسمنا خط تماثل هذه الدالة على نظام الإحداثيات سنلاحظ أنه يقع في المنتصف بين نقاط انعدام الدالة ويقطع المنحنى عند النقطة الصغرى للدالة:
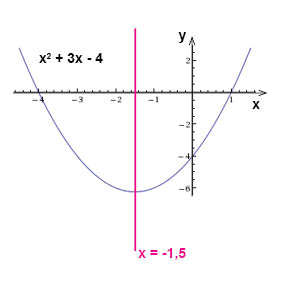
وبما أننا حصلنا على قيمة \(x\) لإحداثيات النقطة الصغرى (قيمة \(x\) على طول خط التماثل)، يمكننا تعويض هذه القيمة في الدالة وايجاد قيمة \(y\) المقابلة (قيمة الدالة عند هذه النقطة) كما يلي:
$$f(-1,5)=(-1,5)^{2}+3\cdot (-1,5)-4=-6,25$$
وهذا يعني أن إحداثيات النقطة الصغرى هي \((-1.5, -6.25)\) والقيمة الصغرى للدالة هي \(-6.25\).
فيديوهات الدرس (باللغة السويدية)
مُقدمة عن دوال الدرجة الثانية.
دوال الدرجه الثانيه ونقاطها العُظمى.
مفهوم القمة (نقطة الانعطاف) ومفهوم خط التماثل.
نقاط انعدام الدالة ونقاط التقاطع مع محور y.
قيّم دوال الدرجة الثانية العُظمى والصُغرى.
