دوال القوى
تناولنا في السابق كيفية وصف الدوال الخطية باستخدام معادلة الخط المستقيم. في هذا القسم سنناقش الدوال الغير خطية التي لا تخضع لأي نوع آخر من العلاقات - فهي عبارة عن دوال غير خطية.
نبدأ بمثال
يمكن وصف السقوط الحر بالدالة التالية
$$s(t)=4,9t^{2}$$
حيث أن \(s\) هي المسافة بالمتر و \(t\) هي الزمن بالثانية.
هذا مثال على دالة القوى. المتغير المُستقل في دوال القوى هو أساس القوة وفي هذا المثال \(t\) هي المُتغير المُستقل.
الصورة العامة لدالة القوى:
$$f(x)=C\cdot x^{n}$$
حيث أن \(C\) و \(n\) ثوابت و \(x\) هي المتغير المُستقل.
إذا كان \(n = 0\) أو \(n = 1\) فستكون الدالة عبارة عن دالة خطية وإذا رسمناها سنحصل على خط مستقيم. بمعنى آخر الدوال الخطية هي حالات خاصة من دوال القوى. فإذا لم تكن الدالة دالة خطية فسيكون لها شكل منحنى ومثل هذه المنحنيات يمكن أن يتغيّر شكلها بصورة كبيرة.
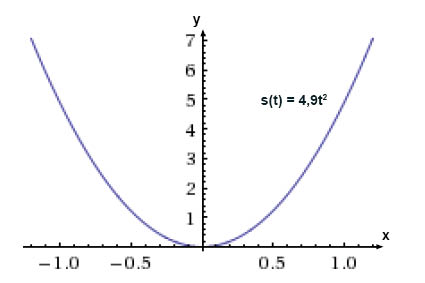
الشكل أعلاه عبارة عن رسم توضحي لدالة السقوط الحر على نظام الإحداثيات. في هذه الحالة لدينا دالة قوى حيث أن قيّم الثوابت هي \(C = 4.9\) و \(n = 2\).
إذا تم تحديد قيمة أي من المتغيّرين \(t\) أو \(s\) سنحصل على معادلة قوى كما درسنا في السابق في الكورس رياضيات 1.
فيديوهات الدرس (بالسويدية)
في هذا الفيديو نستعرض الدوال الأُسية و دوال القوى.
دوال القوى.
