الرسوم البيانية

في في الكورس رياضيات 1 كررنا كيفية استخدام أنظمة الإحداثيات لعرض ووصف النقاط التي لها قيّم لكل من \(x\) و \(y\). في هذا القسم سنواصل في تطوير هذا الموضوع ونستعرض كيف يمكننا استخدام نظام الإحداثيات لعرض وتوضيح عِدة نقاط.

عندما يكون لدينا عِدة نقاط ذات إحداثيات مختلفة يمكن تدوين قيّمها في جدول بيانات كما يلي:

قيّم-\(x\)	قيّم-\(y\)
1	0
2	1
3	0
4	2

يتم تمثيل كل نقطة إحداثية في جدول القيّم باستخدام قيمة \(x\) وقيمة \(y\). جميع هذه النقاط التي تمثل علاقة معينة بهذه الطريقة هي عبارة عن جزء من رسم بياني.

فإذا حددنا هذه النقاط على نظام الإحداثيات ثم وصلناها ببعضها عن طريق رسم خطوط بين كل نقطة والتي تليها في اتجاه \(x\), بالتالي نكون قد أوضحنا الرسم البياني, فهذا يعني أننا قمنا بتوضيح وعرض جزء من مخطط هذه العلاقة في صورة رسم البياني خطي على نظام الإحداثيات:

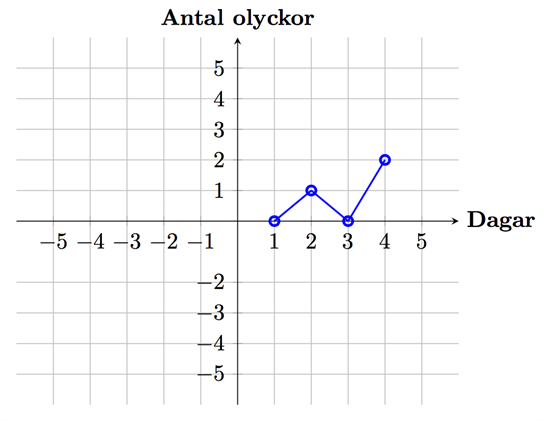
هذا النوع من الرسم يمكن أن يُمثل على سبيل المثال عدد الحوادث في طريقٍ ما لمدة أربعة أيام. فإذا كان محور \(x\) يمثل "الأيام" ومحور \(y\) يمثل "عدد الحوادث" فهذا يعني أننا ألقينا نظرة عامة على حوادث هذا الطريق. توضيح الرسوم البيانية باستخدام نظام الإحداثيات هو طريقة سهلة جدا لإنشاء نظرة سريعة على تطور شيء ما، مثلا في هذه الحالة توضيح التطورات الإحصائية لعدد الحوادث في طريق معين (مع العلم أن هذا المثال يخص فترة زمنية قصيرة جدا).

ليس من الضروري أن تكون التدرجات (التقسيمات) المستخدمة على محور \(x\) مشابهة لتقسيمات محور \(y\) - قد يكون للمحورين مقياس رسم مختلف. وبشكل عام يجب تعديل مقياس الرسم بحيث يتناسب مع حجم القيّم المُراد رسمها. على سبيل المثال إذا كان أجرك (المُرتب) في الساعة 100 كرونة وتريد رسم مخطط بياني لكيفية تغير إجمالي راتبك المالي مع الزمن حسب عدد الساعات التي عملت فيها, سيكون إستخدام نفس مقياس الرسم لكلا المحورين عملية غير مناسبة. ومع ذلك من المهم جدا أن يتم وضع مقياس رسم لكل محور, بمعنى أن يكون لدينا مسافات متساوية بين جميع الوحدات على طول المحور.

فيديو الدرس (باللغة السويدية)

مثال بسيط على الرسم البياني.