Andragradsfunktioner

1. Titta på följande andragradsfunktion och bestäm:

a) funktionens minimumställe

b) vertex koordinater

c) symmetrilinjens ekvation

d) funktionens nollställen

2. Funktionen f(x) = -x² - 6x - 5 är given.

a) Ange grafens symmetrilinje.

b) Har funktionen ett max eller minvärde? Vilket?

c) Vilka koordinater har funktionens vertex?

d) Bestäm funktionens nollställen.

e) kontrollera dina svar genom att rita funktionen grafiskt.

Scrolla ner för lösning!

Lösning:

1.

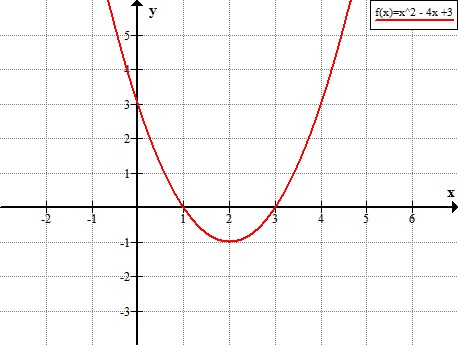
a) Funktionens minsta värde läser vi av på y-axeln och är -1.

b) Vertex är funktionens vändpunkt och är våran minpunkt (2,-1).

c) Vertex ligger på symmetrilinjen. Symmetrilinjens ekvation är x = 2.

d.) Funktionens nollställen betyder då y = 0 och är funktionens rötter. Nollställerna är i punkterna (1,0) och (3,0).

2.

Vi börjar med att lösa andragrads ekvationen -x² - 6x - 5 = 0. Att börja med att lösa denna ekvation ger oss de svar vi behöver.

För att bli av med minustecknet framför x²- termen multiplicerar vi med -1 och får istället x² + 6x + 5 = 0.

Vi kvadrarkompletterar:

x² + 6x + 9 = -5 +9

(x + 3)² = 4

x + 3 = ± 2

x = -3 ± 2

a) När vi tittar på våran lösning x = -3 ± 2 ser vi att nollställerna ligger emellan symmetrilinjen. Det är alltså x = -3 som är vår symmetrilinje.

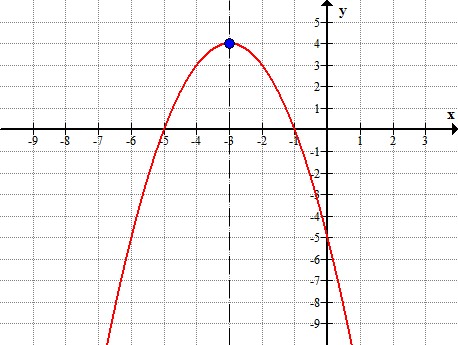
b) Minustecknet framför x²- termen avslöjar redan på en gång att funktionen har ett maxvärde. Vi vet att vårat maxvärde ligger på symmetrilinjen och vi stoppar in x=-3 i funktionen f(-3) = -(-3)² - 6(-3) - 5 = 4

c) Vi får vertex koordinater genom att ta värdet på symmetrilinjen och funktionens maxvärde (som vi fick då vi stoppade in -3 i funktionen) och får punkten (-3,4).

d) Nollställena ligger på punkterna (-5,0) och (-1,0).

e) Grafen har följande utseende: