الدوال المثلثية
لقد قمنا بتعريف كل من الجيب وجيب التمام بناءاً على زاوية حادة في مُثلث قائم الزاوية. وبالتزامن مع شرح مفهوم دائرة الوحدة قمنا بتوسيع تعريف الجيب وجيب التمام بحيث يمكننا التعامل مع الزوايا الأكبر بشكل اعتباطيّ.
في هذا القسم سندرس الدوال المُثلثية وخصائصها بناءاً على ما توصلنا اليه عن الجيب وجيب التمام لزوايا مختلفة. الدوال المُثلثية مفيدة جدا لوصف الظواهر الدورية على سبيل المثال ويحدث ذلك في العديد من السياقات العلمية المختلفة.
دوال الجيب وجيب التمام
بنفس الطريقة التي عرّفنا بها الدوال سابقا باستخدام المتغيرات المستقلة وغير المستقلة يمكننا الآن شرح الدوال المُثلثية. لتكن \(x\) هي المتغير المستقل و\(y\) هي المتغير غير المستقل أو المتغير التابع، حيث يمكننا كتابة دالة الجيب على النحو التالي:
$$y(x)=sin\,x$$
بنفس الطريقة يمكننا كتابة دالة جيب التمام على النحو التالي:
$$y(x)=cos\,x$$
إذا بحثنا مجال ومدي هاتين الدالتين سنلاحظ أن الدالتين مُعرّفتين لجميع الأعداد الحقيقة بينما مداهما (قيمة الدالة) هو
$$-1\leq y(x)\leq 1$$
إذا قمنا برسم هذه الدوال بيانيا على نظام إحداثيات فسنجد أن المنحنيات لها أشكال موجيه ذات قيّم متكررة على فترات منتظمة بناءاً على قيمة المتغير المستقل.
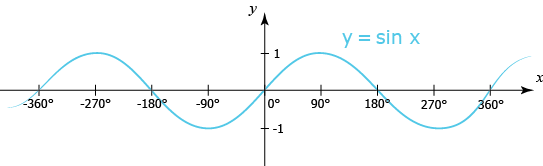
في الشكل أدناه لدينا منحنى جيب الزاوية مرسوم على نظام إحداثي.
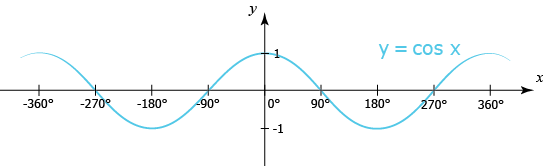
ولدينا في المقابل منحنى جيب التمام كما يلي.
بالنسبة لدالة جيب الزاوية نلاحظ أن \(y(0°)=0\) عندما تكون \(x=0°\). وكلما زادت قيمة \(x\) زادت قيمة الدالة أيضاً. تستمر هذه الزيادة حتى تصل الى \(x=90°\) حيث \(y(90°)=1\). ومن ثم تتناقص قيمة الدالة تدريجيا حتى تصبح \(x=270°\) حيث \(y(270°)=-1\). بعد هذه القيمة الأدنى للدالة تزداد قيمة الدالة مرى أخرى وعند \(x=360°\) ستنعدم قيمة الدالة مره أخرى \(y(360)=0\). بعد هذه القيمة للمتغير سيتكرر هذا النمط عند الفترة \(360°\).
بنفس الطريقة يمكننا دراسة قيّم دالة الجيب عندما تكون وحدة المتغير المستقل \(x\) هي الراديان بدلا من الدرجات. حيث يستلزم ذلك توضيح وحدة المتغير المستقِل.
إذا درسنا دالة جيب التمام ومُنحناها بنفس الطريقة التي درسنا بها دالة الجيب فسرعان ما نُلاحظ أنها مُتماثله مع دالة الجيب مع اختلاف الإزاحة جانباً (قيمة المتغير المستقل) - ويمكن القول أن منحنى جيب التمام يقع على بُعد \(90°\) (\(\frac{π}{2}\) راديان) قبل مُنحنى الجيب لأن الدالتين لهما نفس القيمة إذا أضفنا \(90°\) (\(\frac{π}{2}\) راديان) إلى قيمة المتغير المُستقل لدالة الجيب. على سبيل المثال \(cos 0° = sin 90°\).
السعه
كما توصلنا لذلك بالفعل فان المدى (قيمة الدالة) لكل من دالة الجيب وجيب التمام هو
$$-1\leq y(x)\leq 1$$
يمكننا إذا أردنا تغيير مدى (قيمة الدالة) دالتي الجيب وجيب التمام الى قيّم أُخرى فيمكننا تغيير سعتيهما. أذا بدأنا من دالة الجيب الأصلية
$$y(x)=sin\,x$$
بالتالي يمكننا على سبيل المثال زيادة السعه بالعامل 2 (مُضاعفة السعه) وذلك من خلال كتابة الدالة على النحو التالي:
$$y(x)=2sin\,x$$
هذه الدالة سيكون لها نفس مجال دالة الجيب الأصلية ولكن مداها سيصبح كما يلي
$$-2\leq y(x)\leq 2$$
إذا رسمنا مُنحنى دالة الجيب الأصلية (باللون الأحمر في الشكل أدناه) ومُنحنى دالة الجيب التي سعتها 2 (باللون الأزرق في الشكل) على نفس النظام الإحداثي سنحصل على ما يلي:
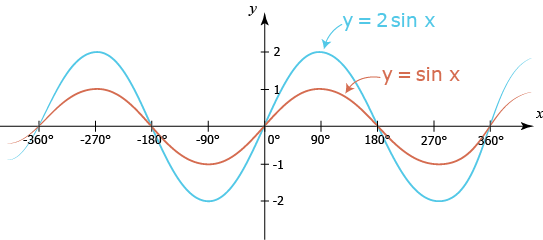
يمكننا بنفس الطريقة القيام بذلك مع دالة جيب التمام والسعات الأُخرى غير الـــــــ 2:
إذا كان مُعطى لدينا مُنحنى الجيب أو جيب التمام مرسوم على نظام إحداثي ولا نعلم تعبير الدالة الجبري، فغالبا ما يكون من السهل تحديد سعة الدالة وذلك من خلال قراءة وحساب نصف الفرق بين القيمة العظمى والصغرى للدالة.
الدورة
كما رأينا سابقا أن دورة دالتي الجيب وجيب التمام هي °360 (\(2\pi\) راديان). ومع ذلك قد نحتاج الى دالة جيب أو جيب تمام لهما دورة أُخرى غير الــــ°360.
يمكن تغيير دورة دالتي الجيب وجيب التمام بتغيير عامل المتغير المستقل في تعبير الدالة. وبالتالي ستكون دالة الجيب
$$y(x)=sin\,2x$$
لها دورة °180 (\(π\) راديان).
يمكن التحقق من أن هذه الدالة لها نصف دورة بمقارنتها بدالة الجيب الأصلية وذلك من خلال مقارنة قيّم مُختلفة للتعبير \(2x\) مع قيّم مختلفة لـ \(x\). بالنسبة لأي قيمة مُعطية للمتغير \(x\) ستكون \(2x\) ضِعف قيمتها، وهذه هي القيمة التي سنحسب القيمة المثلثية لها. بالتالي ستكون دورة هذه الدالة المثلثية عبارة عن نصف دورة.
إذا رسمنا مُنحنى الدالة \(y(x)=sin2x\) على نظام إحداثي سنلاحظ أن تكرار تذبذباته لأعلى ولأسفل ضِعف تكرار تذبذبات دالة الجيب الأصلية وذلك لأن الدالتين لهما دورات مختلفة.
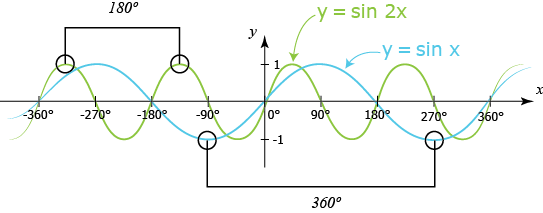
إذ كان لدينا منحنى الجيب أو جيب التمام مرسوم على نظام إحداثي فمن السهل معرفة دورة المُنحنى وذلك من خلال قراءة المسافة الأفقية بين أقرب قمتين للمنحني (القيّم العُظمى للدالة) أو أقرب قاعين (القيّم الصُغرى للدالة). هذه المسافة الأفقية تُمثل دورة الدالة.
كما نلاحظ في الشكل أعلاه فأن دورة الدالة \(y(x)=sinx\) عباره عن °360 بينما دورة الدالة \(y(x)=sin2x\) عباره عن°180.
الإزاحة على مِحوري \(x\) و \(y\)
كما أن دالتي الجيب وجيب التمام يمكن أن يكون لهما سِعات مُختلفة ودورات مُختلفة يمكن أيضا إزاحة منحنييهما على المحور \(x\) و/أو المحور \(y\).
كما نلاحظ أن مُنحنى جيب التمام يمكن رؤيته كمُنحنى جيب تمت إزاحته الى اليسار على النظام الإحداثي أي إزاحة المتغير المستقل بمقدار °90 مُقارنةً بمٌنحنى الجيب الأصلى. ولذلك سيكون لدينا أن
$$y(x)=cos\,x=sin\,(x+{90}^{\circ})$$
وبهذه الطرية يمكننا إزاحة منحني كل من الجيب وجيب التمام على مِحور \(X\) بإضافة أو طرح زاوية الإزاحة المطلوبة للمتغير المستقل. فإذا كان على سبيل المثال لدينا دالة جيب
$$y(x)=sin\,x$$
وأضفنا الزاوية °90 الى \(x\) فسنحصل على
$$y(x)=sin\,(x+{90}^{\circ})$$
وهذا ما يؤدي لإزاحة مُنحناها تجاه اليسار بمقدار °90 أما إذا قمنا بطرح °90 بدلا من الإضافة فسنحصل على
$$y(x)=sin\,(x-{90}^{\circ})$$
مما يؤدي الى إزاحة المُنحنى تجاه اليمين بمقدار 90°.
كما يمكننا أيضا إذا أردنا إزاحة المُنحنى في اتجاه \(y\) بنفس طرية إزاحة الدوال الأُخرى، كالدوال الخطية على سبيل المثال. ليكن لدينا الدالة الخطية التالية
$$y(x)=5x$$
فمن ثم يمكننا إزاحة مُنحنى هذه الدالة خطوة واحدة للأعلى في اتجاه محور \(y\) بإضافة الحد الثابت 1 حيث تصبح الدالة كما يلي
$$y(x)=5x+1$$
بنفس الطريقة يمكننا إزاحة دالة الجيب
$$y(x)=sin\,x$$
خطوة الى الأعلى في اتجاه محور \(y\) وذلك بإضافة 1 إلى تعبير الدالة، حيث نحصل على الدالة التالية
$$y(x)=sin\,x+1$$
كما يمكننا ايضا إزاحة الدالة خطوة الى الأسفل في اتجاه محور \(y\) وذلك بطرح 1 ومنها نحصل على
$$y(x)=sin\,x-1$$
حل المُعادلات المُثلثية بيانياً
كما رأينا سابقًا كيف يمكننا حل المُعادلات المُثلثية باستخدام دائرة الوحدة والدورات, حيث أن هذه المُعادلات غالبا ما يكون لها عِدة حلول.
يمكننا أيضا استخدام الرسم البياني للدالة المُثلثية للحصول على فكرة عن حلولها المحتملة.
دعونا نأخذ مثال
إذا كان لدينا الدالة التالية
$$sin\,3x=\frac{1}{2}$$
فمن ثم يمكننا الحصول على فكرة عن حلولها من خلال رسم المُنحنيين التاليين بيانيا
$$y(x)=sin\,3x$$
و
$$y(x)=\frac{1}{2}$$
وبالتالي جميع نقاط التقاطع بين هاذين المُنحنين ستكون حلول لهذه المعادلة. وهذه في الأساس هي نفس طريقة حل المعادلات بيانيا التي استخدمناها سابقا بالإضافة الى أن الدوال المثلثية عباره عن دوال دورية وهذا ما يجب أن نأخذه في الاعتبار عند تحديد الحلول.
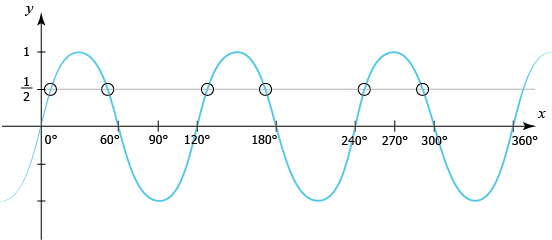
هذه الدالة لها الدورة التالية
$$\frac{{360}^{\circ}}{3}={120}^{\circ}$$
إذا درسنا نقاط تقاطع هذين المُنحيين في الفترة التالية
$${0}^{\circ}\leq x\leq {120}^{\circ}$$
فسنلاحظ أن لدينا تقاطعين: تقاطع عند \(x=10°\) وتقاطع عند \(x=50°\). قيّم \(x\) هذه تُمثل حلول المعادلة.
وبما أن دالة الجيب عبارة عن دالة دورية يمكننا إيجاد حلول أُخرى إذا أخذنا الدورة °120 في الاعتبار. ولذلك فإن هذه المعادلة لها الحلول التالية:
$$x={10}^{\circ}+n\cdot {120}^{\circ}$$
حيث أن n عدد صحيح, و
$$x={50}^{\circ}+n\cdot {120}^{\circ} $$
حيث أن n عدد صحيح.
