تطبيقات التكاملات

في الدورة رياضيات 3 تعلمنا كيف يمكن استخدام التكاملات في عملية حساب المساحة بين مُنحنى الدالة ومحور \(x\). في القسم السابق من هذا الباب رأينا أيضاً أن هنالك عدد من قواعد التكاملات المفيدة.

في هذا القسم سنلقي نظرة قريبة على كيفية تطبيق التكاملات على مسائل مُختلفة في مجالات مُختلفة. تحديدا سننظر الى الربط بين الدوال ودوالها الأولية وكيفية استخدام ذلك في حل المسائل.

عادةً ما تُستخدم التكاملات في مجال العلوم الطبيعية لتحديد الكميات. قد يتعلق الموضوع على سبيل المثال بحساب المسافة عندما يكون لديك دالة السرعة أو عملية حساب السرعة عندما يكون لديك دالة العجلة/التعجيل.

لنأخذ مثال, حيث أن هنالك مركبة تتحرك بُسرعة معروفة كدالة في الزمن. ونريد معرفة المسافة التقي قطعتها السيارة بين نقطتين زمنيتين (بين الثانية الخامسة والثانية العاشرة من بداية حساب الزمن).

كيف يمكننا معرفة ذلك باستخدام حساب متكامل؟

يمكن وصف تغير السرعة في هذه الحالة بالمعادلة التالية

$$v(t)=5\cdot {e}^{0,1t}$$

في الفترة $5\le t\le 10$ ثواني, ويمكن ملاحظة ذلك على نظام الإحداثيات في الشكل التالي.

 

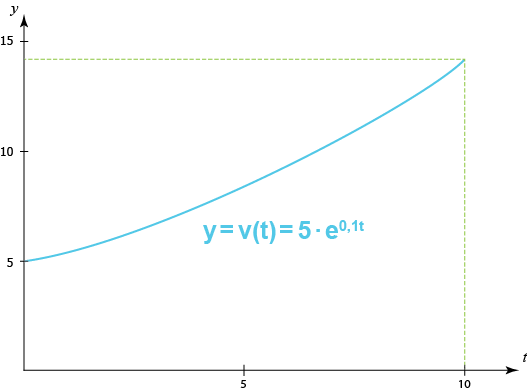
إذا وضعنا ذلك في صيغة التكامل كما يلي

$$\int_{5}^{10}v(t)\,dt=\int_{5}^{10}(5\cdot {e}^{0,1t})\,dt$$

فهذا يعنني أننا سنحسب المساحة تحت المنحنى في الفترة المطلوبة.

بما أن وحدة السرعة هي متر في الثانية (m/s) و وحدة الزمن هي الثواني (s) فهذا يعني أن وحدة التكامل هي المتر (m) وهو ما يعطينا المسافة التي قطعتها المركبة بين النقطة الزمنة "5 ثواني" والنقطة الزمنية "10 ثواني" بسرعة $v\left(t\right)$.

لحساب هذا التكامل علينا أولاً إيجاد الدالة الأولية للدالة $v\left(t\right)$, والتي يُرمز لها بالرمز $V\left(t\right)$. من الدورة رياضيات 3 لدينا قاعدة معروفة لإستخلاص الدالة الأولية للدالة الأُسية, وبالتحديد إذا كان لدينا الدالة التالية:

$$f(x)={e}^{kx}$$

فستكون دالتها الأولية كما يلي

$$F(x)=\frac{{e}^{kx}}{k}+C$$

وبالتالي فسنحصل على الدالة الأولية التالية

$$V(t)=\frac{5\cdot {e}^{0,1t}}{0,1}+C=50\cdot {e}^{0,1t}+C$$

الآن يمكننا حساب قيمة التكامل:

$$s=\int_{5}^{10}(5\cdot {e}^{0,1t})\,dt=V(10)-V(5)=$$

$$=50\cdot {e}^{0,1\cdot 10}+C-(50\cdot {e}^{0,1\cdot 5}+C)=$$

$$=50\cdot {e}^{1}+C-50\cdot {e}^{0,5}-C=$$

$$=50\cdot e-50\cdot \sqrt{e}\approx53\,m $$

إذن المسافة التي قطعتها المركبة بين النقطتين الزمنيتين "$t_1 = 5 s$" و "$t_2 = 10 s$" هي 53متر تقريباً.

---

فيديو الدرس (بالسويدية)

مثال على تطبيق التكاملات.