خطوط التقارب

في القسم السابق درسنا كيف يمكننا رسم الدوال باستخدام مُشتقة الدالة. من المواقف المهمة والتي غالباً ما تنشأ عند رسم مُنحنيات الدوال الغير مُعرّفة لجميع قيّم المتغير المُستقل. هذا هو ما قابلناه في الدورة رياضيات 3 عندما درسنا نهايات الدوال.

في هذا القسم سنُطور هذه المعرفة من خلال معرفة المزيد عن مفهوم خط التقارب وتأثيراته على شكل الدالة.

قد تؤدي بعض الدوال إلى حدوث مشاكل عندما نحاول رسم منحناها بيانياً. وفيما يلي مثال على هذا النوع من الدوال

$$y(x)=\frac{1}{x-1}+2$$

يمكننا مباشرةً ملاحظة أن الدالة غير مُعرفة عند النقطة \(x = 1\) لأن المقام في الحد الأول سيصبح مساوياً للصفر عندما تكون \(x = 1\). أي لا يمكننا حساب قيمة الدالة عند \(x = 1\). ومع ذلك يمكننا التحقق من قيّم الدالة عندما نتحرك على المنحنى انطلاقاً من النقطة \(x = 1\) في الاتجاه السالب أو الموجب.

إذا رسمنا منحنى هذه الدالة على نظام الإحداثيات فسيكون شكله بالقرب من \(x=1\) كما يلي:

 

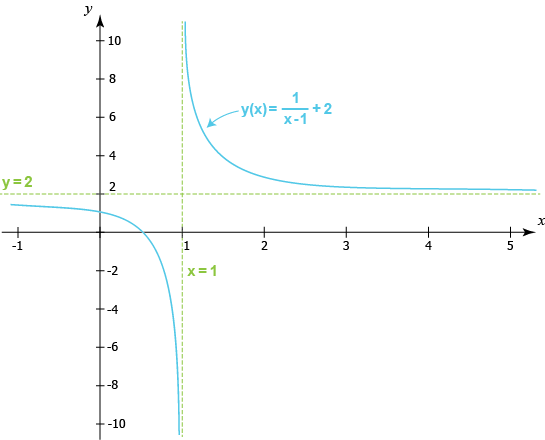
كلما اقتربنا من النقطة \(x=1\) قادمين من الاتجاه السالب كلما تناقصت قيمة الدالة أكثر فأكثر ومن ثم تتجه نحو ما لا نهاية السالبة عندما نقترب أكثر فأكثر من النقطة \(x=1\). وفي هذه الحالة تُكتب نهاية الدالة كما يلي

$$\lim_{x \to 1-}y(x)=\lim_{x \to 1-}\left (\frac{1}{x-1}+2 \right )=-\infty$$

أما إذا اقتربنا من النقطة \(x=1\) قادمين من الاتجاه الموجب فسنلاحظ أن قيمة الدالة تتزايد أكثر فأكثر ومن ثم تتجه نحو ما لا نهاية الموجبة عندما نقترب أكثر فأكثر من النقطة \(x=1\). وفي هذه الحالة تُكتب نهاية الدالة كما يلي

$$\lim_{x \to 1+}y(x)=\lim_{x \to 1+}\left (\frac{1}{x-1}+2 \right )=\infty$$

ما يحدث هنا هو أن الحد الأول في تعبير الدالة سيصبح موجبا متزايداً أو سالبًا متزايداً كلما اقتربنا من النقطة الغير مُعرفة عندها الدالة، أي النقطة \(x\). وذلك لأن قيمة المقام في الحد الأول تصبح أقل وأقل (مع اشارة موجبة أو سالبة).

يمكن اعتبار ما أوجدناه هنا كخط مستقيم عامودي مُعرّف بالنقطة \(x=1\), حيث يقترب منه منحنى الدالة بشكل عشوائي ولكن لا يتقاطع معه أبدا. يُسمى هذا الخط المستقيم بخط التقارب. هذا النوع من الخطوط المقاربة عبارة عن خط مستقيم ولذلك يمكن كتابته كقيمة معينة لــ \(x\) وفي هذه الحالة القيمة هي \(x=1\) ويسمى بخط التقارب الرأسي.

هناك أيضاً خطوط تقارب أفقية تنشأ بطريقة مماثله للخطوط الرأسية. الدالة أعلاه لها خط تقارب أفقي في الحقيقة.

يوجد خط التقارب الأفقي عند أبعد نقطة ممكنه من النقطة الغير مُعرفة \(x=1\) بالقرب من منحنى الدالة: عندما تقترب قيمة \(x\) من ما لا نهاية السالبة أو ما لا نهاية الموجبة. عندما تأخذ \(x\) هذه القيّم سيصبح الحد الثابت 2 هو القيمة المسيطرة للدالة بشكل متزايد حيث أن القيمة المطلقة للحد الأول

$$\frac{1}{x-1}$$

تصبح أصغر وأصغر. ومع ذلك فإن حد التقلص هذا (الحد الأول) لن يأخذ القيمة 0 مهما كانت قيمة \(x\). لذلك لن تأخذ الدالة القيمة 2 أبدا ولكن سوف تقترب بشكل عشوائي من هذه القيمة للدالة والتي بدورها تُشكل خط التقارب الأفقي.

يمكن كتابة ذلك رياضياً كما يلي:

$$\lim_{x \to \pm\infty}y(x)=\lim_{x \to \pm\infty}\left ( \frac{1}{x-1}+2 \right )=2$$

بصورة عامة فإن منحنى الدالة \(y(x)\) يكون له خط تقارب رأسي \(x=a\) عندما يكون

$$\lim_{x \to a-}y(x)=\pm\infty$$

أو

$$\lim_{x \to a+}y(x)=\pm\infty $$

وبالمثل يكون لمنحنى الدالة \(y(x)\) خط تقارب أفقي حيث \(y=b\) عندما يكون

$$\lim_{x \to -\infty} y(x)=b$$

أو

$$\lim_{x \to \infty} y(x)=b$$