إحداثيات الأعداد المركبة

في مقدمة هذا الباب وتحديدا في باب الأعداد المُركبة تعلمنا كيف يمكن كتابة العدد المُركب في صيغة المستطيل $z=a+bi$​, حيث أن $a$ و $b$ عددين حقيقيين و $i$ هي الوحدة التخيلية.

في هذا القسم سنتعلم طرق أخرى لتمثيل الأعداد المركبة باستخدام المحاور الإحداثية للأعداد المركبة.

إحداثيات الأعداد المركبة

إذا كان لدينا عدد حقيقي وليكن $x=3$ مثلاً، فيمكننا تمثيله كنقطة أو موضع على الخط العددي. أما إذا كان لدينا عدد مركب، كالعدد $z=3+2i$ على سبيل المثال فإن الخط العددي لا يكفي لتمثيل هذا العدد بصورة واضحة.

ففي هذه الحالة يمكننا استخدام محاور احداثيات الأعداد المُركبة والذي يمكن توضيحه كإحداثي ديكارتي بحيث يتم تمثيل الجزء الحقيقي من العدد المركب ($Re z$) على محور السينات $x$ والجزء التخيلي من العدد المُركب ($Im z$) على محور الصادات $y$.

بالتالي يمكننا تمثيل الأعداد المركبة على احداثي الأعداد المركبة, إما كنقطة عادية ($Re z, Im z$) أو كسهم يصل بين كل من نقطة الأصل ($0, 0$) والنقطة ($Re z, Im z$).

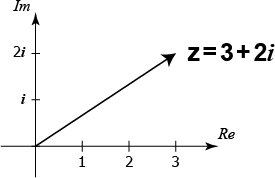
الجمع والطرح على إحداثي الأعداد المُركبة

هناك بعض التشابهات بين تمثيل الأعداد المُركبة على إحداثياتها وتمثيل المتجهات على النظام الإحداثي الديكارتي الطبيعي.

إذا أردنا جمع عددين مركبين فيمكننا تمثيلهما على الإحداثي المُركب بسهمين يبدآن من نقطة الأصل بحيث يشكلان ضلعين من أضلاع متوازي أضلاع ومجموع هذين العددين المركبين هو قطر متوازي الأضلاع.

---

فيما يلي نعرض كيفية تمثيل جمع الأعداد المُركبة على الإحداثي المُركب وذلك من خلال جمع العددين المركبين $z_1$ و $z_2$

حيث أن

$$z_1=-1+2i$$

$$z_2=3+i$$

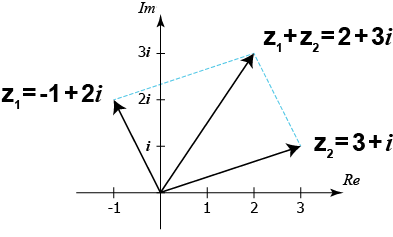
إذن وفقاً لقواعد حساب الأعداد المُركبة فإن مجموع هذين العددين المُركين سيكون كما يلي:

$${z}_{1}+{z}_{2}=(-1+2i)+(3+i)=$$

$$=-1+2i+3+i=$$

$$=2+3i$$

يمكننا بنفس الطريقة طرح عددين مرُكبين وذلك من خلال إضافة سالب العدد المُركب الثاني الـى العدد المُركب الأول. فإذا كان لدينا على سبيل المثال الفرق بين العددين المركبين $z_1=-1+2i$ و $z_2=3+i$, أي $z_1-z_2$ فهذا ما يُعادل $z_1+(-z_2)$.

لذا سنحصل على

$${z}_{1}-{z}_{2}={z}_{1}+(-{z}_{2})=$$

$$=(-1+2i)+(-1)\cdot (3+i)=$$

$$=-1+2i-3-i=$$

$$=-4+i$$

يمكننا تمثيل عملية طرح الأعداد المُركبة على المحاور المُركبة كما يلي:

---

فيديو الدرس (بالسويدية)

تمثيل الأعداد المُركبة على المحاور المُركبة.