رسم الدوال باستخدام المشتقة
في دورة رياضيات 3 تعلمنا كيفية رسم الدوال بيانياً باستخدام مُشتقتها.
في هذا القسم سنتعمق قليلا في مفهوم هذه العلاقة بين مشتقات الدوال وشكل منحنياتها بيانياً على النظام الإحداثي وذلك من خلال دراسة الدوال التي درسناها حتى الآن في الدورة رياضيات 4.
من الدالة إلى المُنحنى
إذا كان لدينا دالة معقدة كما يلي
$$y(x)={x}^{2}\cdot {e}^{-0,4x}-1$$
ونريد رسم هذه الدالة بيانياً في الفترة \(-1 \leqslant x \leqslant 7\) على سبيل المثال فيمكننا القيام بذلك بطُرق مختلفة.
يمكننا اختيار عدد كبير من قيّم المتغير المُستقل ومن ثم حساب قيّم الدالة المقابلة لكل قيمة من قيّم هذا المتغير المُستقل. ومع ذلك فإن هذه الطريقة لا تأخذ في الإعتبار جميع النقاط (الإكثر أهمية من النقاط الأُخرى) في تحديد شكل المنحنى.
ولذلك فإنه من المفيد دراسة قيّم مشتقات الدالة المقابلة لقيّم مختلفة للمتغير المستقل. وفي هذه الحالة يمكننا معرفة قيّم المتغير المُستقل حيث تكون قيّم المُشتقة عندها تساوي الصفر أي عندما تكون الدالة متزايدة أو متناقصة. وبهذه الطريقة يمكننا الحصول على تصور جيّد لشكل منحنى الدالة من خلال استخدام المشتقة وقيّم الدالة عند هذه النقاط المُختارة جيدًا.
لنحاول استخدام هذه الطريقة وتطبيقها على مثال الدالة أعلاه ولهذا سنبدأ باشتقاق الدالة.
نلاحظ أن الدالة تتكون من حدين، حد يحتوي على المتغير \(x\) وحد ثابت. وكما رأينا في رياضيات 3 عندما درسنا أساسيات قواعد الاشتقاق, فإن الدالة التي تتكون من عدة حدود لها مُشتقة تساوي مجموع مشتقات هذه الحدود. ولهذا يمكننا اشتقاق الحدود المتغيرة والحدود الثابتة بصوره منفصلة.
فيما يلي سنشتق الحد المتغير باستخدام قاعدة الضرب وذلك لأن هذا الحد عبارة عن حاصل ضرب دالتين:
$$g(x)={x}^{2}$$
$$h(x)={e}^{-0,4x}$$
لتطبيق قاعدة الضرب علينا اشتقاق هاتين الدالتين أولاً:
$$g'(x)=2x$$
$$h'(x)=-0,4\cdot {e}^{-0,4x}$$
لنشتق الدالة الأصلية (الحد الثابت - 1 سيختفي بالاشتقاق):
$$y'(x)=g'(x)\cdot h(x)+g(x)\cdot h'(x)=$$
$$=2x\cdot {e}^{-0,4x}+{x}^{2}\cdot (-0,4\cdot {e}^{-0,4x})=$$
$$=2x\cdot {e}^{-0,4x}\cdot (1-0,2x)$$
يمكننا الآن دراسة هذه المُشتقة باستخدام قاعدة الضرب الصفري لإيجاد قيّم المتغير المستقل التي ستكون المُشتقة عندها صفراً \(y'(x)=0\):
$$x_1=0 $$
$$x_2=5$$
ستكون النقطتان \((0, y(0))\) و\((5, y(5))\) نقاطاً مُثيره للاهتمام يجب دراستهما عند رسم الدالة بيانياً. نقاط نهايتي فترة التعريف ستكون أيضاً مثيرة للاهتمام، بالتالي سنقوم بحساب كل من \((-1, y(-1))\) و \((7, y(7))\).
إذا قمنا بحساب قيّم الدالة عند هذه النقاط سنحصل على
$$y(-1)={(-1)}^{2}\cdot {e}^{-0,4\cdot (-1)}-1={e}^{0,4}-1\approx0,49$$
$$y(0)={(0)}^{2}\cdot {e}^{-0,4\cdot 0}-1=0-1=-1$$
$$y(5)={(5)}^{2}\cdot {e}^{-0,4\cdot 5}-1=25\cdot {e}^{-2}-1\approx2,38$$
$$y(7)={(7)}^{2}\cdot {e}^{-0,4\cdot 7}-1=49\cdot {e}^{-2,8}-1\approx,1,98$$
سنتعرف أيضا على إشارات المشتقة بين هذه النقاط، لذلك سندرس تعبير مشتقة الدالة. المشتقة التالية تتألف من ثلاثة عوامل وهذه العوامل الثلاثة هي التي ستحدد علامة المشتقة.
$$y\,'(x)=2x\cdot {e}^{-0,4x}\cdot (1-0,2x) $$
العامل الأوسط عبارة عن قوة أساسها العدد \(e\) وهو سيكون دائما موجبا، ولهذا لا نحتاج لإدراج هذا العامل في دراسة إشارات الدالة. بينما سيكون العامل الأول, \(2x\), سالبا لقيّم \(x\) السالبة وموجبا لقيّم \(x\) الموجبة. أما العامل الأخير\((1 - 0.2x)\) سيكون موجبا عندما تكون \(x<5\); وسالبا عندما يكون \(x>5\). بالتالي يمكننا استخلاص جدول الإشارات التالي:
| \(7\) | \(5<x<7\) | \(5\) | \(0<x<5\) | \(0\) | \(-1<x<0\) | \(-1\) | \(x\) |
| \(≈ 1,98\) | تناقص | \(≈ 2,38\) | تزايد | \(-1\) | تناقص | \(≈ 0,49\) | \(y(x)\) |
| سالب | سالب | \(0\) | موجب | \(0\) | سالب | سالب | \(y'(x)\) |
وبالتالي فإن الدالة تتناقص بشدة عندما تكون \(x<0\) وتتزايد بشدة عندما تكون \((0 < x < 5)\) ثم تتناقص مرة أخرى عندما تكون \(x > 5\).
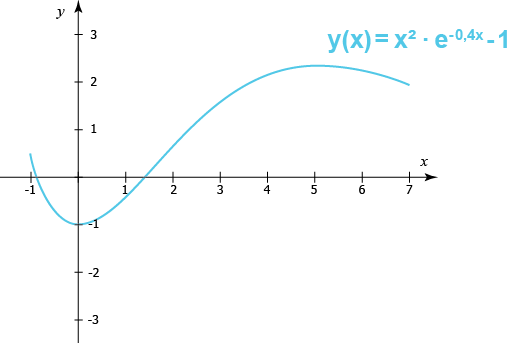
الآن بعد أن أصبح لدينا جدول إشارات يحتوي على معلومات حول قيّم الدالة ومُشتقاتها في الفترة المحددة يمكننا أخيراً رسم مُنحنى الدالة على النظام الإحداثي. ستكون خطوتنا الأولى هي تحديد النقطتين القُصوتين التين أوجدناهما كما يمكننا تحديد نقطتي نهايتي الفترة المُحددة. ومن ثم نرسم منحنى الدالة بين هذه النقاط بإستخدام معلوماتنا عن إشارات الدالة في هذه الفترات المختلفة.
لنحصل على الرسم البياني التالي في الفتر المُحددة بين 1- و 7.
فيديو الدرس (بالسويدية)
في هذا الفيديو سنشرح كيف يمكننا رسم الدوال باستخدام المُشتقة.
