مشتقات بعض الدوال المًهمة

في الدورة رياضيات 3 توصلنا إلى قواعد اشتقاق/تفاضل عدد من تعبيرات الدوال الشائعة وفي هذا القسم سنقوم بتوسيع دراسة مجموعة قواعد الاشتقاق المعروفة بالإضافة الى بعض مشتقات الدوال الهامة.

قواعد اشتقاق لــ \(sin x\) و \(cos x\)

سابقا في هذه الدورة رياضيات 4 درسنا الدوال المثلثية.

$$y(x)=sin\,x$$

و

$$y(x)=cos\,x$$

ويتم استخدام هذه الدوال في العديد من المجالات المختلفة وغالباً ما يكون من المفيد جيداً عندما نكون قادرين على اشتقاق هذه الدوال.

فالدالة

$$y(x)=sin\,x$$

مشتقها هي

$$y\,'(x)=cos\,x$$

والدالة

$$y(x)=cos\,x$$

مشتقتها

$$y\,'(x)=-sin\,x$$

يمكن اشتقاق هاتين الدالتين باستخدام تعريف المشتقة بالمسافة-h والمسح العددي لقيّم النهايات الناشئة.

---

أمثلة على اشتقاق دوال الجيب وجيب التمام

اشتق الدالة التالية.

$$y(x)=3cos\,x$$

يمكننا اشتقاق هذه الدالة مباشرةً وذلك باستخدام قاعدة اشتقاق دالة الجتا \(cosx\) مع مراعاة وجود المعامل 3.

بالتالي فإن مشتقة هذه الدالة هي

$$y\,'(x)=3\cdot (-sin\,x)=-3sin\,x$$

---

اشتق الدالة التالية.

$$y(x)=sin\,2x$$

نلاحظ أن هذه الدالة عبارة عن دالة مركبة ويمكننا كتابتها على النحو التالي

$$y(x)=sin\,(g(x))=f(g(x))=f(u)$$

حيث أن الدالة الخارجية هي

$$f(u)=sin\,u$$

والدالة الداخلية هي

$$u=g(x)=2x$$

ويمكن اشتقاق هذه الدالة المركبة باستخدام قاعدة السلسة ولذلك سنقوم باشتقاق كل من الدالة الخارجية والدالة الداخلية بصوره منفصلة.

الدالة الخارجية

$$f(u)=sin\,u$$

يمكن اشتقاقها بالنسبة لـــ \(u\) كما يلي

$$f'(u)=cos\,u$$

الدالة الداخلية

$$g(x)=2x$$

يمكن اشتقاقها بالنسبة لـــ \(x\) كما يلي

$$g'(x)=2$$

بالتالي يمكن الحصول على مشتقة الدالة المركبة باستخدام قاعدة السلسة

$$y\,'(x)=f'(g(x))\cdot g'(x)=$$

$$=(cos\,2x)\cdot 2=$$

$$=2cos\,2x$$

---

اشتق الدالة التالية.

$$y(x)=cos\,\left (\frac{\pi}{4}-x \right )$$

هذه أيضاً دالة مركبة ويمكن كتابتها على النحو التالي

$$y(x)=cos\,(g(x))=f(g(x))=f(u)$$

حيث أن الدالة الخارجية هي

$$f(u)=cos\,u$$

والدالة الداخلية هي

$$u=g(x)=\frac{\pi}{4}-x$$

بنفس الطريقة كما في المثال السابق يمكن استخدام قاعدة السلسلة لاشتقاق هذه الدالة المركبة ولذلك سنقوم بإيجاد مشتقة كل من الدالة الداخلية والدالة الخارجية.

الدالة الخارجية

$$f(u)=cos\,u$$

يمكن اشتقاقها بالنسبة لـــ \(u\) كما يلي

$$f'(u)=-sin\,u$$

الدالة الداخلية

$$g(x)=\frac{\pi}{4}-x$$

يمكن اشتقاقها بالنسبة لـــ \(x\) كما يلي

$$g'(x)=-1$$

بالتالي يمكننا الحصول على مشتقة الدالة المركبة باستخدام قاعدة السلسة

$$y\,'(x)=f'(g(x))\cdot g'(x)=$$

$$=-sin\,\left ( \frac{\pi}{4}-x \right )\cdot (-1)=$$

$$=sin\left ( \frac{\pi}{4}-x \right )$$

قواعد اشتقاق الدوال الأٌسية

في دورة رياضيات 3 تعرفنا على العدد e كأساس يجعل الدالة الأُسية

$$y(x)={e}^{x}$$

لها مشتقة

$$y\,'(x)={e}^{x}$$

إذا رسمنا هذه الدالة الأُسية على نظام إحداثي فسيكون شكلها على النحو التالي:

 

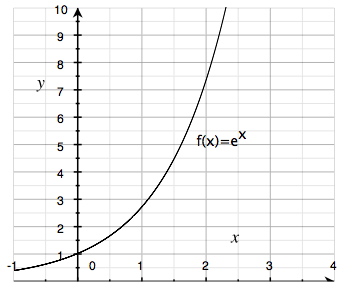
كما نلاحظ أن هذه الدالة الأُسية متزايدة بصورة دائمة لجميع قيّم المتغير \(x\), أي أن مشتقتها دائما موجبة. يمكننا أيضًا استخلاص هذا الاستنتاج من خلال دراسة تعبير مشتقة الدالة.

سابقاً توصلنا أيضا إلى أن الصيغة العامة للدالة الأُسية ذات الأساس e

$$y(x)={e}^{kx} $$

حيث أن \(k\) ثابت, لها مشتقة

$$y\,'(x)=k\cdot {e}^{kx}$$

وفي هذه الحالة ليست بالضرورة أن تكون الدالة متزايدة بصورة دائمة، حيث أن قيّم الثابت \(k\) قد تكون سالبة. إذا أخذ الثابت \(k\) قيمة سالبة فستكون الدالة تناقصية بشكل تام – كما أن مشتقة الدالة ستكون سالبة لجميع قيم المتغير \(x\).

إذا أخذ أساس الدالة الأسية قيمة عشوائية a فيمكننا كتابتها كما يلي

$$y(x)={a}^{x}$$

يمكن إعادة كتابة تعبير هذه الدالة باستخدام تعريف اللوغاريتم الطبيعي وذلك من خلال كتابة قيمة a كما يلي

$$a={e}^{ln\,a}$$

ومن ثم تعويض قيمة a في أساس الدالة الأُسية لنحصل على

$$y(x)={a}^{x}={({e}^{ln\,a})}^{x}={e}^{(ln\,a)\,\cdot x}$$

وأي معادلة مكتوبة بهذه الطريقة يمكن اشتقاقها بنفس طريقة الدالة التالية

$$y(x)={e}^{kx}$$

حيث أن

$$k=ln\,a$$

ولهذا فإن الدالة الأسية

$$y(x)={a}^{x}$$

مشتقها كما يلي

$$y\,'(x)=(ln\,a)\cdot {e}^{(ln\,a)\,\cdot x}$$

بما أن

$$a={e}^{ln\,a}$$

يمكننا كتابة هذه المشتقة بدلالة الأساس a كما يلي:

$$y\,'(x)=(ln\,a)\cdot {a}^{x}$$

لقد درسنا مشتقة هذه الدالة في دورة رياضيات 3 حيث درسنا ميزات العدد e.

بصورة عامة يمكن استخلاص أن الدالة الأسية

$$y(x)={a}^{kx}$$

حيث أن الأساس a عبارة عن قيمة عشوائية و \(k\) ثابت, يمكن اشتقاقها كما يلي

$$y\,'(x)=k\cdot (ln\,a)\cdot {a}^{kx}$$

قواعد اشتقاق الدوال اللوغاريتمية

إذا كان لدينا دالة في الصيغة التالية

$$y(x)=log\,x$$

أو

$$y(x)=ln\,x$$

فإن هذا النوع من الدوال يُسمى بالدوال اللوغاريثمية.

بصورة عامة هذا النوع من الدوال مُعّرف فقط عند القيّم الموجبة للمتغير المستقل ,أي أن \(x>0\).

الدالة اللوغاريتمية

$$y(x)=ln\,x$$

حيث أن \(x>0\)

$$y\,'(x)=\frac{1}{x}$$

بما أن المتغير \(x\) يأخذ القيّم الموجبة فقط فإن المُشتقة أيضا تأخذ دائما القيّم الموجبة؛ ولهذا فإن هذه الدالة اللوغاريتمية ستكون في حالة تزايد بصوره دائمة لجميع قيّم المتغير \(x\) المُحددة.

ملخص

لنلخص الآن مشتقات الدوال التي قابلناها في هذا القسم في الجدول التالي.

الدالة	مُشتقتها
\(sin \, x\)	\(cos \, x\)
\(cos \, x\)	\(-sin \, x\)
\(e^{kx}\)	\(k \cdot e^{kx}\)
\(a^{kx}\)	\(ln \, a \cdot k \cdot a^{kx}\)
\(ln \, x\)	\(\frac{1}{x}\)