الصّيغ المثلثيه

في الأقسام السابقة كررنا العلاقات المثلثية الأساسية ورأينا كيف يمكن حل المُعادلات المُثلثية البسيطة.

في هذا القسم سنُقدم عدد من الصِيّغ المُثلثية التي ستساعدنا في حل المُعادلات المُثلثية.

صيغة فيثاغورث المُثلثية

إذا بدأنا من دائرة الوحدة فمن ثم يمكن تحديد أي نقطة على محيط الدائرة بحيث تكون النقطة كما يلي:

$$P=(cos\,v,\,sin\,v)$$

حيث أن $v$ هي الزاوية التي تشير بشكل واضح الى النقطة $P$ أي هي الزاوية التي يصنعها الخط الواصل بين نقطة الأصل والنقطة $P$.

يمكننا صياغة العلاقة بين $\cos v$ و $\sin v$ باستخدام نظرية فيثاغورث.

نعلم أن دائرة الوحدة لها نصف قطر طوله 1 وحدة طول وهو الذي يُشكل وتر مثلث قائم الزاوية، كما هو الحال بالنسبة للنقطة $P$ في الرُبع الأول لدينا مُثلث رؤوسه هي النقاط $P(\cos v, \sin v)$ و $(\cos v, 0)$ و نقطة الأصل $(0, 0)$.

حيث أن طول الضلع القائم الأول هو $\left|\cos v\right|$ وطول الضلع القائم الثاني هو $\left|\sin v\right|$

بما أننا نعلم أطوال أضلاع المُثلث فبالتالي يمكننا صِياغة نظرية فيثاغورس بناء على أطوال هذه الأضلاع المعروفة:

$${(sin\,v)}^{2}+{(cos\,v)}^{2}={1}^{2}$$

ويمكن تبسيط هذه العلاقة كما يلي

$$sin^{2}v+cos^{2}v=1$$

حيث أن ${\sin }^{2}v$ و${\cos }^{2}v$ عبارة عن رموز تعبيريه لكل من ${\left(\sin v\right)}^2$ و${\left(cosv\right)}^2$ على التوالي وهذه التعبيرات ستُستخدم من الآن فصاعدا.

هذه العلاقة التي تمت صياغتها تُسمى بمتطابقة فيثاغورث المُثلثية.

---

لنأخذ الآن مثال على استخدام صيغة فيثاغورث المُثلثية.

أثبت صحة المعادلة المُثلثية التالية باستخدام صيغة فيثاغورث المُثلثية.

$$1-{cos}^{2}x={(tan\,x\cdot cos\,x)}^{2}$$

يمكن إثبات صحة هذه العلاقة من خلال إعادة كتابة الطرف الأيمن لنرى إن كان سيُعادل الطرف الأيسر. لذا سنحاول تبسيط الطرف الأيمن باستخدام العلاقة بين الدوال المُثلثية

$$tan\,x=\frac{sin\,x}{cos\,x}$$

بالتالي يمكننا إعادة كتابة الطرف الأيمن للمعادلة كما يلي

$${(tan\,x\cdot cos\,x)}^{2}={\left (\frac{sin\,x}{cos\,x}\cdot cos\,x \right )}^{2}=$$

$$={(sin\,x)}^{2}={sin}^{2}x$$

وهذا التعبير المُبسط يمكننا إعادة كتابته باستخدام المتطابقة المُثلثية الأولى:

$${sin}^{2}x+{cos}^{2}x=1$$

$${sin}^{2}x+{cos}^{2}x-{\color{Blue} {{cos}^{2}x}}=1-{\color{Blue} {{cos}^{2}x}}$$

$${sin}^{2}x=1-{cos}^{2}x$$

وهذا ما يُعادل بالضبط طرف المعادلة الأصلية الأيسر.

بالتالي تم إثبات صحة المعادلة المُثلثية

---

صِيّغ الجمع والطرح

بالإضافة إلى متطابقة فيثاغورث المُثلثية هناك عدد من الصِيّغ المُثلثية التي توضح كيف يمكن إعادة كتابة التعبيرات المُثلثية التي تحتوي على جمع أو طرح الزوايا.

لأي زاويتين $v$ و $w$ لدينا العلاقات المُثلثية التالية:

$$sin(v+w)=sin\,v\cdot cos\,w+cos\,v\cdot sin\,w$$

$$sin(v-w)=sin\,v\cdot cos\,w-cos\,v\cdot sin\,w$$

$$cos(v+w)=cos\,v\cdot cos\,w-sin\,v\cdot sin\,w$$

$$cos(v-w)=cos\,v\cdot cos\,w+sin\,v\cdot sin\,w$$

$$tan(v+w)=\frac{tan\,v+tan\,w}{1-tan\,v\cdot tan\,w}$$

$$tan(v-w)=\frac{tan\,v-tan\,w}{1+tan\,v\cdot tan\,w}$$

---

دعونا نأخذ مثال نستخدم فيه إحدى هذه الصِيغ.

حِل المعادلة التالية باستخدام صِيغة الجمع للجيب.

$$sin\,(x+{90}^{\circ})=\frac{1}{2}$$

نعيد كتابة الطرف الأيسر من المعادلة باستخدام صِيغة الجمع للجيب.

$$sin\,(x+{90}^{\circ})=sin\,x\cdot cos\,{90}^{\circ}+cos\,x\cdot sin\,{90}^{\circ}$$

$\cos {90}^{°}$ و $\sin {90}^{°}$ لها قيّم مُثلثية معروفة وهي:

$$cos\,{90}^{\circ}=0$$

$$sin\,{90}^{\circ}=1$$

وهذا ما يُسهل لنا عملية تبسيط الطرف الأيسر من المعادلة الأصلية:

$$sin\,x\cdot cos\,{90}^{\circ}+cos\,x\cdot sin\,{90}^{\circ}=$$

$$=sin\,x\cdot 0+cos\,x\cdot 1=$$

$$=0+cos\,x=$$

$$=cos\,x$$

الآن لدينا نُسخة مُبسطة من المعادلة الأصلية وهي كما يلي:

$$cos\,x=\frac{1}{2}$$

هذه المُعادلة المُثلثية لها حلول معروفة: حل يمكن حسابه باستخدام الآلة الحاسبة مباشرةً وحل آخر يمكن استخراجه من دائرة الوحدة.

$$x=arccos\,\left ( \frac{1}{2} \right )=\pm{60}^{\circ}$$

بما أن فترة $\cos v$ هي${360}^{°}$ فستكون الحلول الكاملة للمعادلة كما يلي:

$$x_1={60}^{\circ}+n\cdot {360}^{\circ}=$$

$$x_2={300}^{\circ}+n\cdot {360}^{\circ}=$$

حيث $n$ عدد صحيح
$n=1, 2, 3, \dots$

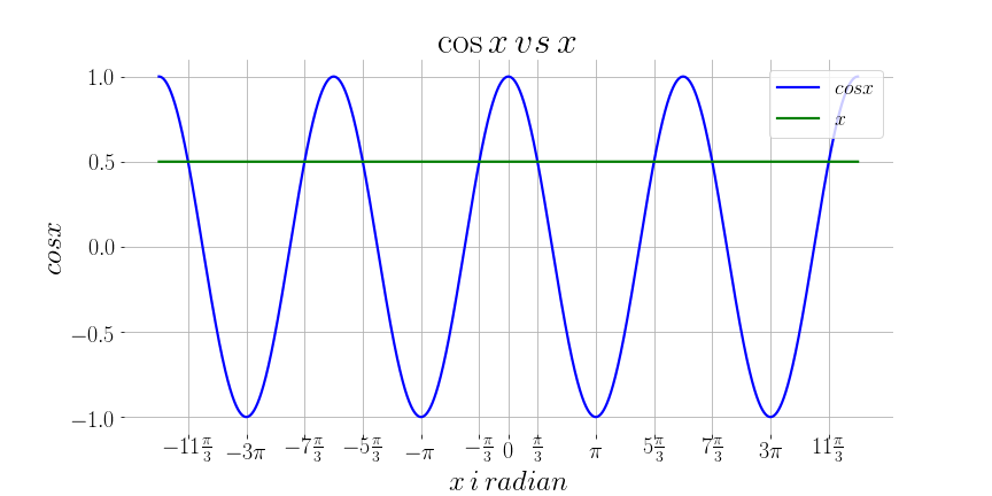
فيما يلي الحلول البيانية للدالة في الفترة \(-11\frac{\pi}{3} \leqslant x \leqslant 11\frac{\pi}{3}\), حيث يتقاطع الخط \(x = 0,5\) مع المُنحنى \(cosx\).

---

صِيّغ ضعف الزاوية

الآن بعد أن قمنا بصياغة الجمع والطرح يمكننا استنتاج جيب وجيب تمام ضعف الزاوية.

إذا كان هنالك زاويتين متساويتين نريد جمعهما فسيكون لدينا

$$v+v=2v$$

فمن ثم سيكون جيب وجيب تمام ضعف الزاوية كما يلي

$$sin\,2v=2\cdot sin\,v\cdot cos\,v$$

$$cos\,2v={cos}^{2}v-{sin}^{2}v$$

يمكننا إعادة كتابة صِيغة جيب تمام ضِعف الزاوية باستخدام مُتطابقة فيثاغورث المُثلثية كما يلي

$$cos\,2v={cos}^{2}v-{sin}^{2}v=$$

$$=2\cdot {cos}^{2}v-1=$$

$$=1-2\cdot {sin}^{2}v$$

يمكن اشتقاق صِيغة جيب ضعف الزاوية باستخدام صِيغة الجمع لجيب الزاوية.

$$sin\,2v=sin\,(v+v)=$$

$$=sin\,v\cdot cos\,v+cos\,v\cdot sin\,v=$$

$$=2\cdot sin\,v\cdot cos\,v$$

بنفس الطريقة يمكننا اشتقاق صِيغة جيب تمام ضِعف الزاوية:

$$cos\,2v=cos\,(v+v)=$$

$$=cos\,v\cdot cos\,v-sin\,v\cdot sin\,v=$$

$$={cos}^{2}v-{sin}^{2}v$$

---

لنأخذ مثال على كيفية استخدام إحدى صِيغ ضِعف الزاوية.​

أثبت صحة العلاقة التالية باستخدام صِيغة جيب تمام ضِعف الزاوية

$$\frac{cos\,2x}{{cos}^{2}x}=1-{tan}^{2}x$$

سنركز على الطرف الأيسر حيث يمكننا تطبيق صِيغة جيب تمام ضِعف الزاوية على البسط:

$$\frac{cos\,2x}{{cos}^{2}x}=\frac{{cos}^{2}x-{sin}^{2}x}{{cos}^{2}x}=$$

$$=\frac{{cos}^{2}x}{{cos}^{2}x}-\frac{{sin}^{2}x}{{cos}^{2}x}=1-\frac{{sin}^{2}x}{{cos}^{2}x}$$

الآن نلاحظ أن الواحد موجود في المكان المناسب، لذا علينا فقط إعادة كتابة الحد الثاني:

$$\frac{{sin}^{2}x}{{cos}^{2}x}=\frac{sin\,x\cdot sin\,x}{cos\,x\cdot cos\,x}=$$

$$=tan\,x\cdot tan\,x={tan}^{2}x$$

الآن وصلنا إلى العلاقة المطلوبة:

$$\frac{cos\,2x}{{cos}^{2}x}=1-{tan}^{2}x$$