الأعداد المركبة في الصيغة القطبية

في مقدمة هذا الباب وتحديدا في باب الأعداد المُركبة تعلمنا كيف يمكن كتابة العدد المُركب في صيغة المستطيل $z=a+bi$, حيث أن $a$ و $b$ عددين حقيقيين و $i$ هي الوحدة التخيلية. كما رأينا أيضاُ كيف يمكن تمثيل الأعداد المُركبة على الإحداثي المٌركب سوآءً في شكل نقطة فقط أو كسهم واصل بين نقطة الأصل والنقطة المُركبة.

في هذا القسم سنعرض طريقة أخرى لكتابة الأعداد المُركبة بصورة واضحه وبالتحديد طريقة الصورة القُطبية. كتابة الأعداد المُركبة في الصورة القُطبية يجعل عمليتي ضرب وقسمة الأعداد المُركبة أسهل من أجراءهما في حالة صيغة المُستطيل.

الصيغة القطبية

بما أنه يمكن تمثيل العدد المُركب $z=a+bi$ بوضوح على الإحداثي المُركب سوآءا بنقطة أو بسهم بين نقطة الأصل والنقطة الإحداثية المُركبة فمن الممكن أيضا كتابة العدد المركب بدلالة كل من طول السهم الواصل بين نقطة الأصل والنقطة المُركبة والزاوية المحصورة بين السهم ومحور الجزء الحقيقي ($Re$). كتابة العدد المُركب $z$ بهذه الطريقة يعني أننا كتبناه في الصيغة القطبية.

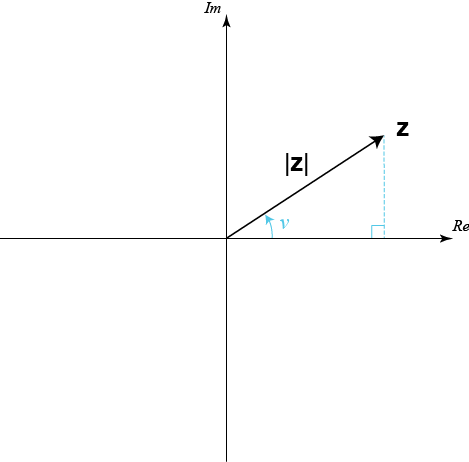
بالتالي لكي نتمكن من كتابة العدد المُركب $z$ في الصورة القطبية سنحتاج إلى طول السهم ومقدار الزاوية.

القيمة المطلقة $\left|z\right|$

يمكننا حساب طول السهم للعدد المُركب بنفس الطريقة كما في حالة حساب أطوال المتجهات وطول السهم هو القيمة المطلقة للعدد المُركب $\left|z\right|$. يمكننا إنشاء مثلث قائم الزاوية باستخدام طول سهم العدد المُركب الواصل بين نقطة الأصل ونقطة رأس السهم والذي بدوره يُمثل وتر المثلث، والجزء الحقيقي والجزء التخيلي من العدد المُركب يُمثلان الضلعين المتعامدين في المُثلث. وبالتالي يمكننا حساب القيمة المطلقة للعدد المُركب باستخدام نظرية فيثاغورس:

$${|z|}^{2}={a}^{2}+{b}^{2}$$

$$|z|=\sqrt{{a}^{2}+{b}^{2}}$$

فإذا كان لدينا على سبيل المثال العدد المُركب $z=8+6i$ فستكون القيمة المطلقة لهذا العدد المُركب كما يلي:

$$|z|=\sqrt{{8}^{2}+{6}^{2}}=\sqrt{64+36}=\sqrt{100}=10$$

سعة العدد المركب z

لكتابة العدد المركب $z$ في الصورة القطبية سنحتاج أيضًا إلى معرفة الزاوية بين سهم العدد المُركب (الواصل بين نقطة الأصل ونقطة العدد المركب) ومحور الجزء الحقيقي ($Re$). تُسمى هذه الزاوية بسعة العدد المُركب أو سعة $z$ وتُكتب $\mathit{a}\mathit{r}\mathit{g}\mathbf{ }\mathit{z}$.

يمكن حساب سعة العدد $z$ باستخدام العلاقات المثلثية الأساسية. إذا رمزنا إلى الزاوية بين سهم العدد المُركب ومحور الجزء الحقيقي بالرمز $v$ فيمكننا كتابة العلاقة التالية للعدد المركب $z$ في الربع الأول

$$tan\,v=\frac{b}{a}$$

حيث أن $b$ هو الجزء التخيلي و $a$ هو الجزء الحقيقي. وهذا ما يعطينا الزاوية

$$v=arctan\,\left (\frac{b}{a} \right )$$

فإذا كان لدينا على سبيل المثال العدد المركب $z=8 + 6i$ فستكون سعة العدد $z$ في هذه الحالة مساويةً لـ

$$v=arctan\,\left (\frac{6}{8} \right )\approx{37}^{\circ}$$

ومن هذا المُنطلق يمكننا التعبير عن العدد الحقيق بـــــ $Re z=a$ والتخيلي بـ $lm z=b$ وتعتمد قيّمهما على القيمة المطلقة $\left|z\right|$ و سعة العدد $z$.

يمكننا كتابة

$$sin\,v=\frac{b}{|z|}$$

وهذا ما يعطينا

$$b=|z|\cdot sin\,v$$

بنفس الطريقة يمكن كتابة

$$cos\,v=\frac{a}{|z|}$$

وهو ما يعطينا

$$a=|z|\cdot cos\,v$$

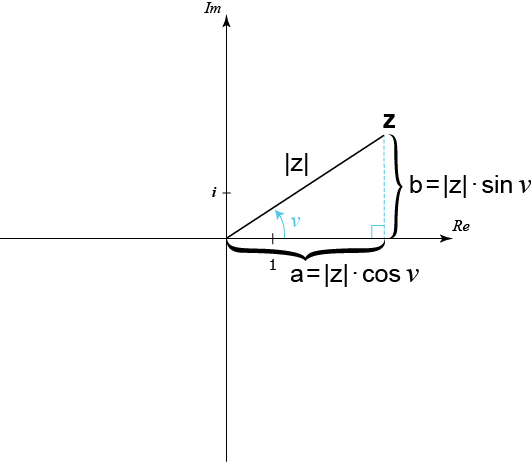
بصورة عامة يمكن كتابة أي عدد مركب $z=a+bi$ على النحو التالي

$$z=|z|\cdot cos\,v+i\cdot |z|\cdot sin\,v=$$

$$=|z|\cdot (cos\,v+i\cdot sin\,v)$$

وهذه هي الصورة القطبية للعدد المُركب $z$.

باستخدام المصطلحات أعلاه يمكننا تمثيل العدد المركب على الإحداثي المُركب على النحو التالي:

---

أكتب العدد المركب أدناه في صيغته القطبية.

$$z=-2+i$$

لكتابة العدد المُركب في الصورة القطبية سنحتاج إلى معرفة كل من القيمة المطلقة للعدد $z$ وسِعته. يمكن أن نرى القيمة المطلقة للعدد المُركب وسِعته في الشكل التالي:

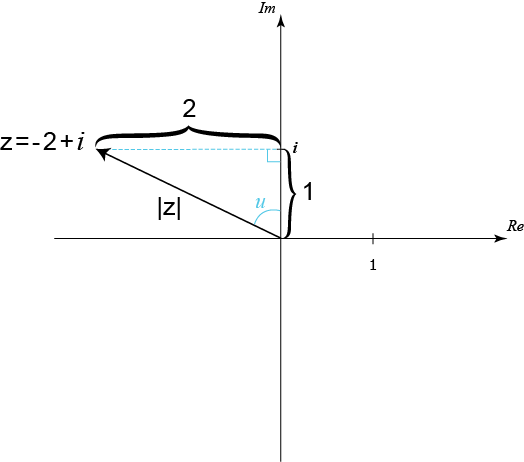
لنحسب القيمة المطلقة للعدد $z$ كما يلي

$$|z|=\sqrt{{a}^{2}+{b}^{2}}=\sqrt{{(-2)}^{2}+{1}^{2}}=\sqrt{5}$$

أصبحت سعة العدد المُركب $z$ أكثر تعقيدًا لأن العدد المركب يقع الآن في الربع الثاني.

يمكننا إنشاء مثلث قائم الزاوية في الربع الثاني، حيث لدينا زاوية حادة

$$u=arctan\,\left (\frac{|a|}{|b|} \right )=arctan\,\left ( \frac{2}{1} \right )\approx {63}^{\circ}$$

أي أن سِعة العدد $z$ تساوي

$$v=u+{90}^{\circ}\approx{153}^{\circ}$$

بالتالي يمكننا كتابة الصورة القطبية للعدد المُركب $z$ كما يلي

$$z=|z|\cdot (cos\,v+i\cdot sin\,v)\approx$$

$$\approx\sqrt{5}\cdot (cos\,{153}^{\circ}+i\cdot sin\,{153}^{\circ})$$

---

أكتب العدد المركب التالي في صيغة المستطيل.

$$z=3\cdot (cos\,{240}^{\circ}+i\cdot sin\,{240}^{\circ}) $$

لكتابة العدد $z$ في صيغة المستطيل سنحتاج إلى معرفة كل من الجزء الحقيقي والجزء التخيلي.

نبدأ بتحديد القيمة المطلقة للعدد المركب وسعته:

$$|z|=3$$

$$v={240}^{\circ} $$

بما أن سعة الدد المُركب هي ${240}^{°}$ فهذا يعني أن العدد المُركب يقع في الربع الثالث للاحداثي المركب. لذلك يمكننا إنشاء مثلث قائم الزاوية في الربع الثالث، حيث يكون طول وتره 3 وحدات طولية والزاوية الحادة $u$ بين الوتر والجزء السالب للمحور الحقيقي هي

$$u=v-{180}^{\circ}={240}^{\circ}-{180}^{\circ}={60}^{\circ}$$

وفق للشكل أدناه.

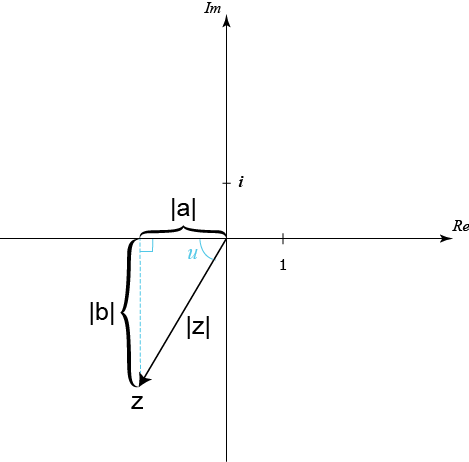
يمكننا الآن حساب أطوال الضلعين القائمين للمثلث $\left|a\right|$ و $\left|b\right|$ حيث يأخذان قيّم موجبة:

$$cos\,{60}^{\circ}=\frac{|a|}{|z|}$$

$$|a|=|z|\cdot cos\,{60}^{\circ}=3\cdot cos\,{60}^{\circ}=1,5$$

و

$$sin\,{60}^{\circ}=\frac{|b|}{|z|}$$

$$|b|=|z|\cdot sin\,{60}^{\circ}=3\cdot sin\,{60}^{\circ}\approx2,6$$

ولكن بما أن هذا العدد المركب $z$ يقع في الربع الثالث فان قيمة كل من الجزء الحقيقي والجزء التخيلي ستكون سالبة, حيث نحصل على

$$a=(-1)\cdot |a|=-1,5 \\b=(-1)\cdot |b|\approx-2,6$$

بالتالي يمكننا كتابة العدد المركب $z$ في صيغة المستطيل على النحو التالي

$$z\approx-1,5-2,6i $$