العلاقات المُثلثية
لقد سبق أن درسنا العلاقات المثلثية الأساسية في الدورتين رياضيات 1 ورياضيات 3 وفي هذا القسم والقسم التالي سنكرر بعض ما تعلمناه سابقا، كما سنتعمق أيضا في حساب المُثلثات بصورة أكثر تفصيلاً.
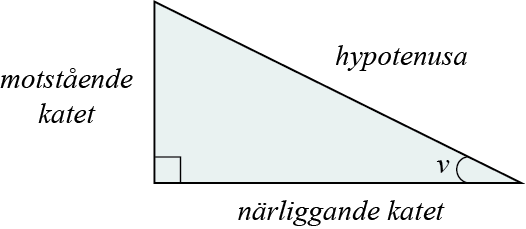
في أي مثلث قائم الزاوية عادة ما يكون لدينا علاقات مُثلثيه متوقعة بين أحد زوايا المثلث الحادة وحاصل القسمه بين ضلعين من أضلاع المثلث. هذه العلاقات درسناها سابقا كما ذكرنا وهي كما يلي:
$$sin\,v=\frac{motstående\,katet}{hypotenusan} $$
$$cos\,v=\frac{närliggande\,katet}{hypotenusan}$$
$$tan\,v=\frac{motsående\,katet}{närliggande\,katet}$$
| اللغة العربية | اللغة السويدية |
| الضلع المُقابل | motstående katet |
| الضلع المُجاور | närliggande katet |
| الوتر | hypotenusan |
تختلف قيمة هذه النسب بين ضلعي المثلث حسب حجم الزاوية الحادة. عادة ما يكون ناتج هذه القسمة بالنسبة لزوايا معينة عباره عن قيمة مضبوطة وهذا ما قد يكون مفيد في عدد من السياقات الرياضية٠
إذا كان على سبيل المثال لدينا مثلث كبير متساوي الأضلاع ومقدار كل زاويه من زواياه °60 وقمنا بتقسيمه الى مثلثين كما في الشكل أدناه فسنلاحظ أن المثلث القائم الزاوية الأيمن يمكن رؤيته كنصف المثلث الأكبر المتساوي الأضلاع الذي طول كل ضلع من أضلاعه 1 وحدة طولية.
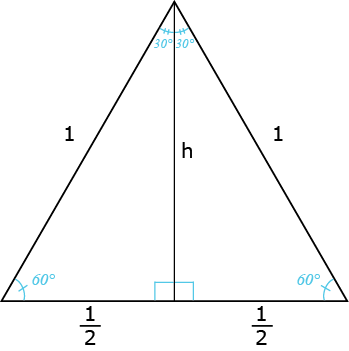
باستخدام نظرية فيثاغورس يمكننا حساب قيمة ارتفاع المثلث بدقه:
$${1}^{2}=\left (\frac{1}{2} \right )^{2}+{h}^{2}$$
$$h=\sqrt{{1}^{2}-\left ( \frac{1}{2} \right )^{2}}=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}$$
من هذا المُثلث القائم الزاوية يمكننا حساب القيّم المُثلثية بدقه لكل من ظل الزاوية °60 tan, جيب الزاوية °60 sin, وجيب تمام الزاوية °60 cos.
$$tan\,{60}^{\circ}=\frac{h}{\frac{1}{2}}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\frac{\sqrt{3}}{2}\cdot \frac{2}{1}=\sqrt{3}$$
$$sin\,{60}^{\circ}=\frac{h}{1}=\frac{\sqrt{3}}{2}$$
$$cos\,{60}^{\circ}=\frac{\frac{1}{2}}{1}=\frac{1}{2}$$
بنفس الطريقة والدِقة يمكننا استنتاج القيّم المُثلثية لزوايا أُخرى مُختلفة المقدار، في الجدول أدناه لدينا القيّم المُثلثية الدقيقة للزوايا الأكثر شيوعاً:
| $$tan \, v$$ | $$cos \, v$$ | $$sin \, v$$ | $$v$$ |
| $$0$$ | $$1$$ | $$0$$ | $$0^{\circ}$$ |
| $$\frac{1}{\sqrt3}$$ | $$\frac{\sqrt3}{2}$$ | $$\frac{1}{2}$$ | $$30^{\circ}$$ |
| $$1$$ | $$\frac{1}{\sqrt2}$$ | $$\frac{1}{\sqrt2}$$ | $$\frac{1}{\sqrt2}$$ |
| $$\sqrt3$$ | $$\frac{1}{2}$$ | $$\frac{\sqrt3}{2}$$ | $$\frac{1}{2}$$ |
| $$-$$ | $$0$$ | $$1$$ | $$0$$ |
فيديو الدرس (باللغة السويدية)
في هذا الفيديو سنرى كيف يمكننا تحديد زاوية مجهوله في مثلث باستخدام حساب المُثلثات والعلاقة بين الوتر و أحد أضلاع المُثلث.
