المخططات البيانية

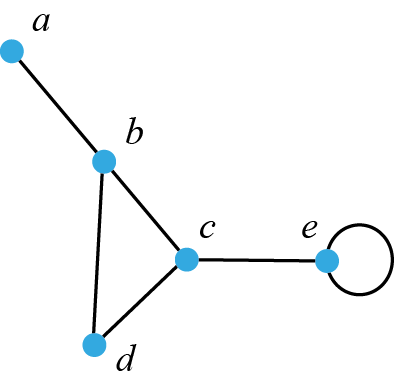
في الصورة أعلاه تم تمييز رؤوس المُخطط باستخدام النقاط والحروف $a$, $b$, $c$, $d$, $e$ والأضلاع بخطوط تصل بين رؤوس المُخطط. يتألف هذا المُخطط من مجموعتي الرؤوس والأضلاع التاليتين، حيث أن مجموعة الأضلاع يتم وصفها بأزواج الرؤوس التي يربطها هذا الضلع:

$$V=\{a,\,b,\,c,\,d,\,e\}$$

$$E=\{\{a,\,b\},\,\{b,\,c\},\,\{b,\,d\},\,\{c,\,d\},\,\{c,\,e\},\,\{e,\,e\}\}$$

نقول أن الرأسين $x$ و$y$ ($x$ لا تساوي $y$) مُتَجاورين إذا كان بينهما ضلع واحد على الأقل. ففي المُخطط أعلاه على نلاحظ أن الرأس $b$ على سبيل المثال له ثلاثة رؤوس متجاورة $a$, $b$ و$c$, وذلك لأن مجموعة الأضلاع E تحتوي على العناصر $\left\{a, b\right\}$, $\left\{b, c\right\}$ و $\left\{b, d\right\}$.

يختلف مفهوم الرؤوس والأضلاع من سياق الى سياق، أي أن معناهما يعتمد على السياق. إذا كان لدينا على سبيل المثال مشكلة في مجال النقل والمواصلات، ففي هذه الحالة يمكن أن تكون المدن أو نقاط تقاطع حركة المرور عبارة عن رؤوس أو زوايا المُخطط (المجموعة V), والطرق أو وسائل الاتصال الأخرى التي تربط المدن/نقاط التقاطع هي الأضلاع (المجموعة E). وفي مثل هذا السياق يمكننا على سبيل المثال إيجاد أقصر طريق بين أي مدينتين أو أقصر طريق يمكن استخدامه لزيارة مجموعة معينة من المدن.

عملية رسم وتوضيح المخططات بالطريقة أعلاه تعمل بشكل جيد عندما نتعامل مع مخططات صغيرة نسبيا، ولكن عندما يزداد عدد الرؤوس والأضلاع ستصبح هذه الطريقة غير عملية لحل المسائل.

---

ارسم صورة المُخطط الذي يتكون من مجموعتي الرؤوس والأضلاع التالية.

$$V=\{a,\,b,\,c,\,d,\,e\}$$ $$E=\{\{a,\,b\},\,\{b,\,c\},\,\{c,\,d\},\,\{d,\,a\},\,\{c,\,e\},\,\{d,\,e\}\}$$

نلاحظ أن لدينا خمسة عناصر في مجموعة الرؤوس وستة عناصر في مجموعة الأضلاع. وبالتالي ستحتوي الصورة على خمس رؤوس وستة أضلاع.

إذا نظرنا الى مجموعة الأضلاع سنلاحظ أن الأربعة أضلاع الأولى تربط بين الرؤوس $a$, $b$, $c$, $d$ حيث أن الرأس $a$ له ضلع مشترك مع $b$, الرأس $b$ له ضلع مشترك مع $c$, الرأس $c$ له ضلع مشترك مع $d$ والرأس $d$ له ضلع مشترك مع $a$. وهذا يعني أنه يمكننا رسم هذا الجزء من المُخطط كشكل رباعي رؤوسه $a$, $b$, $c$, $d$:

وبهذا نكون قد رسمنا الأربعة أضلاع الأولى من مجموعة هذه الأضلاع. الضلعان المتبقيان من مجموعة الأضلاع $\left\{c, e\right\}$ و $\left\{d, e\right\}$ يربطان الرأسين $c$ و$d$ بالرأس $e$. يمكن إدراج هذا في الرسم بإضافة الرأس $e$ حيث أن النقاط $e$, $c$ و$d$ تُشكل رؤوس مثلث:

الآن تم رسم المُخطط باستخدام جميع رؤوس مجموعة الرؤوس وجميع أضلاع مجموعة الأضلاع.

---

الرؤوس والأضلاع

يبدأ ضلع المُخطط البياني عند رأس وينتهي عند رأس. بالتالي يمكننا وصف ضلع المخطط البياني باستخدام الرموز الرياضية التي تعلمناها في باب نظرية المجموعات على النحو التالي.

$$\{x,\,y\}\,\,\,d\ddot{a}r\,x\in V\,och\,y\in V$$

قد تكون بداية الضلع عند رأس ونهايته عند رأس أخر، أي $\left(x\ne y\right)$ وقد تكون بدايته عند راس ونهايته عند نفس الرأس وفي هذه الحالة $\left(x=y\right)$. الضلع الذي يبدأ وينتهى عند نفس الرأس يُسمى بالحلقة. في بداية هذا القسم لدينا مثال على الحلقة حيث أن لدينا ضلع $\left\{e, e\right\}$, الذي يبدأ وينتهي عند الرأس $e$.

قد توجد عدة أضلاع تربط بين نفس أزواج الرؤوس في بعض السياقات. قد يحدث هذا على سبيل المثال في حالة المدن والطرق التي تربط بينها، حيث يمكنك أن تتخيل أن هناك عدة طُرق مختلفة تربط بين نفس المدينتين.

عدد الأضلاع المتصلة بالرأس هي التي تحدد درجة أو تكافؤ الرأس. في المُخطط البياني الأول في بداية هذا القسم نلاحظ أن الرأس $a$ من الدرجة 1, الرأس $d$ من الدرجة 2 والرؤوس $b$ , $c$ و $e$ من الدرجة 3 (الرأس $e$​ له الدرجة 3 لأن له ضلع مشترك مع الرأس $c$ بالإضافة الى ضلعي بداية ونهاية الحلقة عند الرأس $e$).

عندما تكون درجة الرأس عدد فردي نقول أن هذا الرأس فردي؛ أما إذا كانت درجة الرأس عدد زوجي فنقول أن هذا الرأس زوجي. تحديد ما إذا كانت الرؤوس فردية أم زوجية مفيد عندما نقوم بتحليل وجود ما يسمى طرق أويلر ودوائر أويلر في المُخططات البيانية وهذا ما سندرسه لاحقا في هذا الباب.

فيديو الدرس بالسويدية