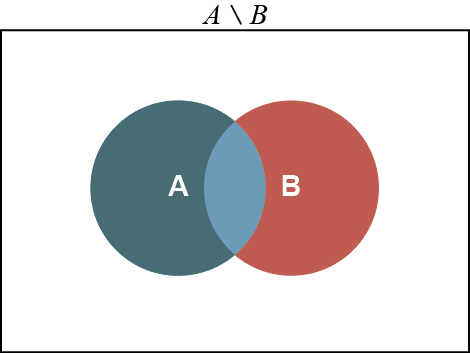
أشكال ڤن - Venndiagram
سابقا في هذا الباب شرحنا أحد أهم المفاهيم وهو مفهوم المجموعة كما ناقشنا عدد من عمليات المجموعات (المتممة، الاتحاد، التقاطع والفرق).
في هذا القسم سنتعلم كيف يمكننا تمثيل المجموعات باستخدام أشكال ڤن-Venndiagram. كما سندرس أيضا كيف يمكن توضيح المجموعات الناتجة من عمليات المجموعات المختلفة عن طريق هذه الأشكال.
أشكال ڤن- Venndiagram
أشكال ڤن- Venndiagram هي احدى الطُرق المستخدمة لتوضيح المجموعات. عادة ما يتم تمثيل المجموعات في شكل ڤن- Venndiagram بدوائر، حيث يتم رسم هذه الدوائر داخل مستطيل, وهذا المستطيل بدوره يُمثل المجموعة الشاملة لهذه المجموعات.
فإذا أردنا على سبيل المثال توضيح المجموعتين و بحيث يحتويان على عنصر واحد مشترك على الأقل (أي أن هناك عنصر واحد على الأقل موجود في كلا المجموعتين و ), ففي هذه الحالة يمكننا تمثيلهما على شكل ڤن- Venndiagram التالي:
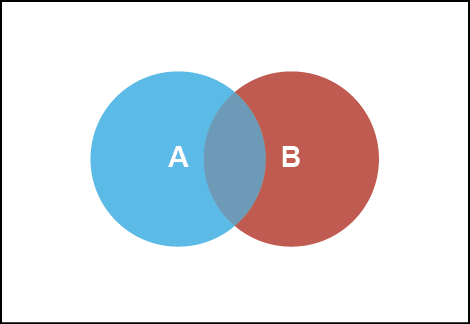
يمكن الإشارة الى اشتراك المجموعتين و في عنصر واحد على الأقل بدوائر متداخلة. نلاحظ أن هذا الشكل يوضح ثلاثة مناطق جزئية: منطقة العناصر التي تنتمي إلى المجموعة ولا تنتمي إلى , منطقة العناصر التي تنتمي إلى المجموعة ولا تنتمي إلى ومنطقة العناصر التي تنتمي إلى كلا المجموعتين و معاً.
أما إذا لم يكن هناك عنصر مشترك بين المجموعتين و ، فيمكننا بدلاً من ذلك توضيح المجموعتين باستخدام مخطط ڤن-Venndiagram التالي:
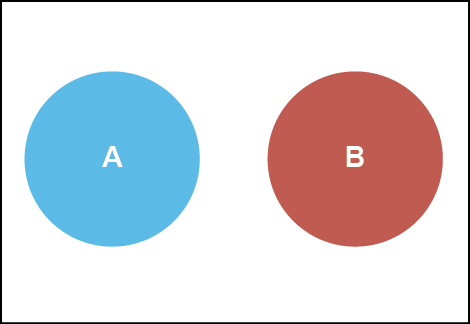
وفي هذه الحالة لا تتداخل الدوائر مع بعضها البعض.
فيما يلي لدينا شكل ڤن-Venndiagram فيه ثلاثة دوائر تمثل المجموعات , و, وجميعها متداخلها مع بعضها البعض وتُشكل سبعة مناطق مختلفة:
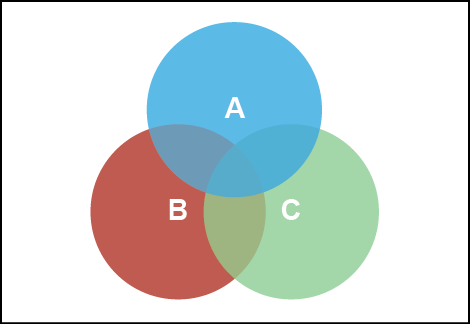
العمليات على المجموعات وأشكال ڤن-Venndiagram
في القسم السابق ناقشنا عمليات المجموعات الأربعة المهمة: المجموعة المتممة, الاتحاد, التقاطع والفرق.
يمكننا توضيح كل عملية من هذه العمليات باستخدام مخطط ڤن-Venndiagram.
- المجموعة المتممة هي المجموعة التي تحتوي على جميع العناصر التي لا تنتمي للمجموعة . يتم تمثيل هذه المجموعة في مخطط ڤن-Venndiagram بالمساحة التي تقع خارج الدائرة كما يلي.

- اتحاد المجموعتين و هو المجموعة التي تحتوي على جميع العناصر الموجودة في أو أو كليهما. يتم تمثيل هذه المجموعة في شكل ڤن-Venndiagram بالمنطقة التي تحتوي على الدائرتين و معاً:

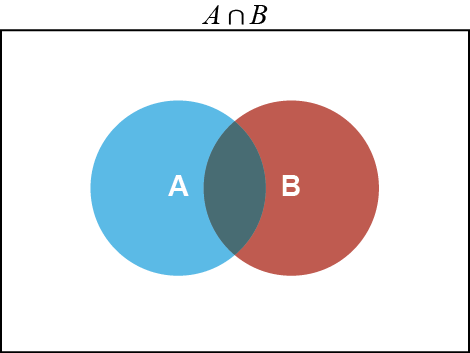
- تقاطع المجموعتين و هو المجموعة التي تحتوي على جميع العناصر الموجودة في كل من و . ويتم تمثيل هذه المجموعة في شكل ڤن-Venndiagram بالمنطقة التي يتداخل فيها الدائرتين و مع بعضهما البعض:
- الفرق بين المجموعتين و هو المجموعة التي تحتوي على جميع العناصر التي تنتمي الى ولا تنتمي الى . ويتم تمثيل هذه المجموعة في شكل ڤن-Venndiagram بمنطقة الدائرة التي لا تتداخل مع الدائرة :