مبدأ الضرب

في هذا الباب سنتعرف على أساسيات ومفهوم التباديل والتوافيق وذلك من خلال دراسة كل من مبدأ الضرب, التباديل والتوافيق.

سنبدأ هذا الباب بدراسة مبدأ الضرب وكيفية استخدامه في عملية حساب عدد الطُرق الممكنة لاختيار عنصر مَّا من بين مجموعتين أو أكثر من مجموعتين.

مبدأ الضرب

في باب نظرية المجموعات تعرفنا على مفهوم المجموعة.

فإذا كان لدينا مجموعتين $\mathbf{A}$ و $\mathbf{B}$ ونريد معرفة عدد الطرق المختلفة التي يمكننا بها اختيار عنصرين، عنصر من المجموعة $\mathbf{A}$ وعنصر من المجموعة $\mathbf{B}$, ففي هذه الحالة يمكننا استخدام مبدأ الضرب.

ينص مبدأ الضرب على أنه إذا كان هناك $x$ طريقة لإجراء الاختيار الأول و $y$ طريقة لإجراء الاختيار الثاني فبالتالي سيكون هناك $xy$ طريقة ممكنة لإجراء هاذين الاختيارين معاً.

فإذا كان الاختيار الأول سيكون عنصر من عناصر المجموعة $\mathbf{A}$ والاختيار الثاني عنصر من عناصر المجموعة $\mathbf{B}$, ففي هذه الحالة سيكون هنالك $\left|\mathbf{A}\right|$ طريقة مختلفة لاختيار عنصر من المجموعة $\mathbf{A}$, كما سيكون هنالك $\left|\mathbf{B}\right|$ طريقة مختلفة لاختيار عنصر من المجموعة $\mathbf{B}$ (حيث $\left|\mathbf{A}\right|$ هي كاردنالية $\mathbf{A}$ و $\left|\mathbf{B}\right|$ هي كاردينالية $\mathbf{B}$, والكاردنالية هي عدد عناصر المجموعة). بالتالي وفقاً لمبدأ الضرب يمكننا اختيار عنصرين بحيث يكون أحدهما من المجموعة $\mathbf{A}$ والآخر من المجموعة $\mathbf{B}$ بـ $\left|A\right|\mathbf{·}\left|B\right|$ طريقة.

فإذا اردنا على سبيل المثال اختيار عنصر من المجموعة $\mathbf{A}=\left\{a, b, c\right\}$ وعنصر من المجموعة $\mathbf{B}=\left\{1, 2, 3, 4\right\}$ فيمكن القيام بذلك على النحو التالي: $$\begin{matrix}(a,\,1), & (a,\,2), & (a,\,3), & (a,\,4), \\(b,\,1), & (b,\,2), & (b,\,3), & (b,\,4), \\(c,\,1), & (c,\,2), & (c,\,3), & (c,\,4)\end{matrix}$$

حيث أن $(c, 3)$ تعني أننا اخترنا العنصر $c$ من المجموعة $\mathbf{A}$ والعنصر $3$ من المجموعة $\mathbf{B}$.

من القائمة أعلاه نلاحظ أن عدد الطُرق هو $12$ طريقة ولكن كان يمكننا حساب عدد الطُرق باستخدام كارديناليتي المجموعتين:

$$|A|\cdot |B|=3\cdot 4=12$$

يمكن توضيح هذا الموقف باستخدام طريقة مخطط الشجرة، حيث أولا نختار عنصر من $\mathbf{A}$ ثم عنصر من $\mathbf{B}$ على النحو التالي:

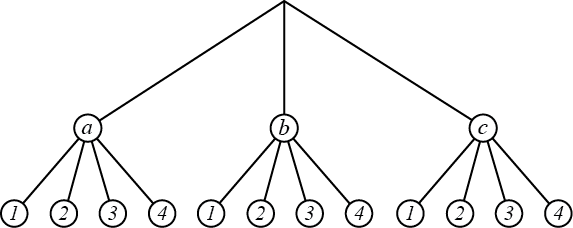
في هذا المثال كان لدينا اختيارين (اختيار عنصر من كل مجموعة) ولكن يمكن توسيع مبدأ الضرب لأكثر من اختيارين بكل سهولة. فإذا اردنا على سبيل المثال اختيار عنصر من كل مجموعة من المجموعات $\mathbf{A}$, $\mathbf{B}$ و $\mathbf{C}$ فيمكن اختيار العنصر الأول بـ $\left|A\right|$ طريقة والعنصر الثاني بـ $\left|B\right|$ طريقة والعنصر الثالث بـ $\left|C\right|$ طريقة وهذا ما يعني أن اختيار مجموعة تتكون من ثلاثة عناصر, عنصر من $\mathbf{A}$ ,عنصر من $\mathbf{B}$ وعنصر من $\mathbf{C}$ سيتم بــ $\left|A\right|\mathbf{·}\left|B\right|\mathbf{·}\left|C\right|$ طريقة مختلفة.

نلاحظ أيضا أنه أردنا حساب عدد طُرق الاختيار فإن ترتيب الاختيارات لا يهم وذلك لأن $\mathbf{\left|}\mathbf{A}\mathbf{\right|}\mathbf{·}\mathbf{\left|}\mathbf{B}\mathbf{\right|}\mathbf{=}\mathbf{\left|}\mathbf{B}\mathbf{\right|}\mathbf{·}\mathbf{\left|}\mathbf{A}\mathbf{\right|}$.

---

لدى أنتون بنطلونين وأربع قمصان وثلاثة روابط عنق. كم عدد الطُرق التي يمكنه بها اختيار بنطلونين وقميص ورباط عنق واحد؟

يمكننا حل هذه المسألة باستخدام مبدأ الضرب.

لتكن مجموعة البناطلين هي المجموعة $\mathbf{A}$, مجموعة القمصان هي $\mathbf{B}$ ومجموعة روابط العنق هي $\mathbf{C}$. ونعلم أن المجموعة $\mathbf{A}$ تحتوي على عنصرين، المجموعة $\mathbf{B}$ تحتوي على أربعة عناصر والمجموعة $\mathbf{C}$ تحتوي على ثلاثة عناصر وهذا يعني أن كاردينالية المجموعات هي $\left|A\right|=2$, $\left|B\right|=4$ و $\left|C\right|=3$.

يمكننا حساب عدد الطُرق المُمكنة لهذه الاختيارات الثلاثة باستخدام مبدأ الضرب على النحو التالي:

$$|A|\cdot |B|\cdot |C|=2\cdot 4\cdot 3=24$$

أي أن لدى أنتون في هذه الحالة $24$ طريقة مختلفة لاختيار بنطلونين وقميص ورباط عنق واحد.

---

أكواد المنتجات

قررت شركة إنشاء نظام بحيث يكون لكل منتج كود وذلك لكي يتم تعريف كل منتج بكل بسهولة من خلال هذا الكود. لقد فكر أفراد الشركة في أن كل كود من أكواد المنتجات عبارة عن حرفين وخمسة أرقام ولكن لا يعلمون عدد المنتجات التي ستغطيها هذه الاكواد.

ما هو عدد المنتجات التي يمكن تعريفها باستخدام هذا النظام؟ بافتراض أن الحروف التي يمكن استخدامها هي جميع حروف اللُغة السويدية ما عدا الحروف $å$, $ä$ و$ö$ والأرقام هي من $0$ إلى $9$.

الحل:

وفقاً لشكل الأكواد المطلوبة سنختار أولا حرف ثم حرف آخر وأخيراً نختار خمسة أرقام من بين الأرقام $0$ إلى $9$.

يمكننا اعتبار أن لدينا مجموعتين $\mathbf{A}$ و $\mathbf{B}$, بحيث تكون عناصر المجموعة $\mathbf{A}$ هي مجموعة الحروف المسموح بها وعناصر المجموعة $\mathbf{B}$ هي مجموعة الأرقام المسموح بها. بالتالي أولا سنختار حرفين من عناصر المجموعة $\mathbf{A}$ ثم اختيار خمس أرقام من عناصر المجموعة $\mathbf{B}$.

عدد حروف اللُغة السويدية بدون الحروف $å$, $ä$ و$ö$ هي $26$ حرفاً. بالتالي لدينا $26$ عنصرا في المجموعة $\mathbf{A}$, أي أن $\left|A\right|=26$

الأعداد من $0$ إلى $9$ هي $10$ أرقام وهي التي تُمثل عدد عناصر المجموعة $\mathbf{B}$​, أي أن $\mathbf{B}=10$

يمكن اختيار الحرفين الأولين بـ ${26}^2$ طريقة مختلة، وذلك لأننا سنختار حرفين من بين مجموعة تحتوي على $26$ عنصر.

يمكن اختيار كل رقم من الأرقام الخمسة في الكود بـ $10$ طُرق مختلفة، وذلك لأننا سنستخدم عشرة أرقام وهي من $0$ إلى $9$. وهذا يعني أن هناك ${10}^5$ طريقة مختلفة لاختيار الخمسة أرقام.

بالتالي جميع الاختيارات عبارة عن سبعة اختيارات (حرفين وخمسة أرقام) سيتم اختيارها مستقلة عن بعضها البعض، وكما ينص مبدأ الضرب يمكننا حساب عدد الطُرق الممكنة لاختيار هذه الخانات السبعة على النحو التالي:

$${|A|}^{2}\cdot {|B|}^{5}={26}^{2}\cdot {10}^{5}=676\cdot 100\,000=67\,600\,000$$

وهذا يعني أن هذا النظام يمكنه إنشاء $67,6$ مليون كود. إذا لم تتوقع الشركة أن يكون لديها منتجات أكثر من ذلك، فإن عدد الأكواد هذا سيكون كافياً لاحتياجات الشركة.

---

فيديو الدرس بالسويدية