المسارات والدورات

سابقا في هذا الباب تعرفنا على النظرية المركزية للمخططات البيانية, حيث تعرفنا على مفهوم المُخطط البياني وبعض خضائصه. في القسم السابق أيضا درسنا مفهوم الطرق والمسارات والدوائر على المُخططات البيانية, كما تعلمنا كيف يمكننا تحديد ما إذا كان المُخطط البياني يحتوي على مسار و/أو دائرة أويلر.

في هذا القسم سنشرح مفاهيم المسار والدورة بالإضافة الى ما يُسمى بمسارات ودورات هاميلتون.

المسارات والدورات

في القسم السابق شرحنا مفهوم الجولة وهو الحركة من خلال رؤوس المخططات البيانية.

$${v}_{1},\,{v}_{2},\,...\,,\,{v}_{n}$$

حيث أن الرؤوس المتتالية متجاورة (أي بينهما ضلع). أذا لم يكن هناك ضلع تم تجاوزه أكثر من مرة ففي هذه الحالة تُسمى الجولة بالطريق

إذا تم عبور رؤوس الطريق مرة واحدة فقط ففي هذه الحالة يُسمى الطريق بالمسار أو الدرب. علاوة على ذلك إذا انتهى المسار/الدرب عند نفس الرأس الذي بدأ منه ففي هذه الحالة يُسمى المسار بالدورة. بالتالي جميع الدورات عبارة عن مسارات/دروب في حين ان المسار/الدرب ليس من الضروري أن يكون دورة.

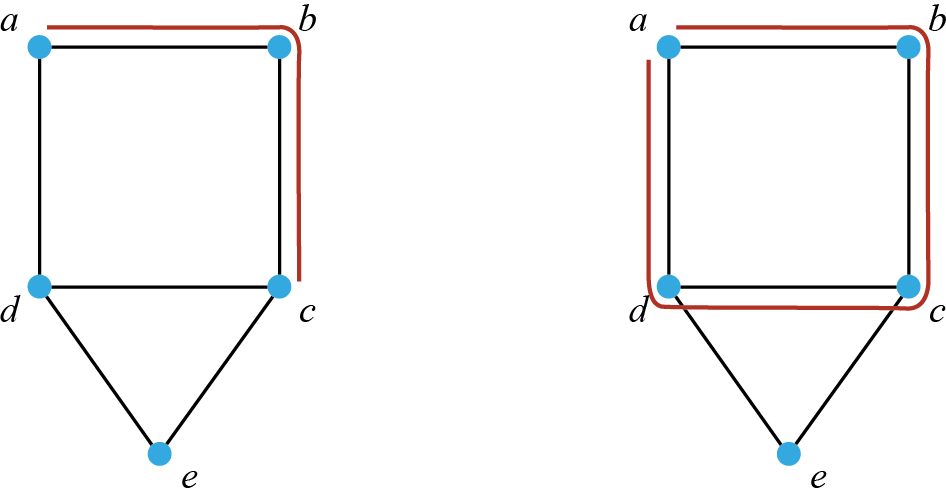
في القسم السابق رأينا المُخطط البياني التالي:

في الأشكال التالية لدينا أمثلة لكل من المسار والدورة على المُخطط أعلاه. على اليسار لدينا مثال على المسار/الدرب وهو المسار $(a, b, c)$, وعلى اليمين لدينا مثال على الدورة وهي الدورة $(a, b, c, d, a)$:

مسارات هاميلتون ودورات هاميلتون

خرج أحد زُعماء الأحزاب في حملة انتخابية وقرر زيارة عدد من المدن مرة واحدة أثناء جولته بدون العودة اليها مرة أخرى.

يمكننا تحليل هذه المسألة باستخدام مُخطط بياني, حيث تُمثل الرؤوس المُدن المحددة بينما الأضلاع تُمثل طُرق الرحلات بين هذه المدن.

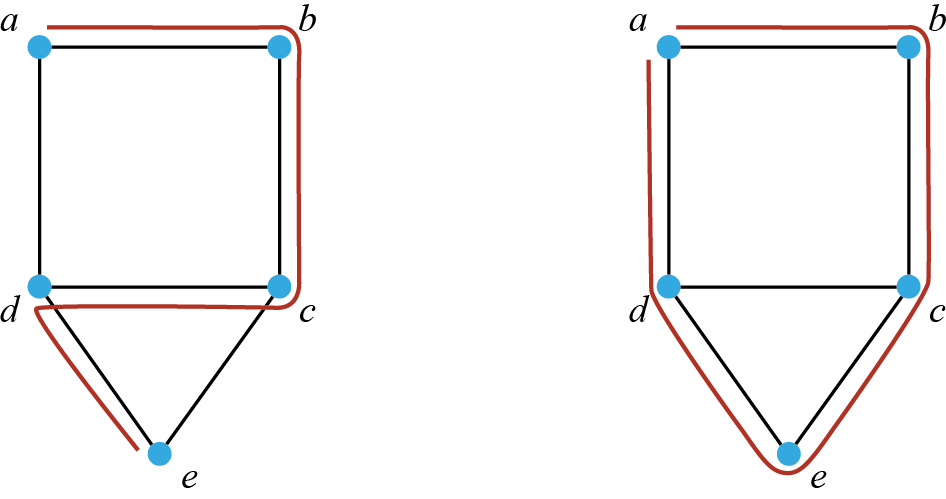
ما نبحث عنه هو مسار يتم فيه زيارة كل ركن من أركان المُخطط البياني مرة واحدة فقط. يُسمي هذا المسار بمسار هاميلتون نسبة لعالم الرياضيات ويليام هاميلتون William R. Hamilton.

مسار هاميلتون الذي يبدأ وينتهي عند نفس الرأس يُسمى بدورة هاميلتون.

في المُخطط البياني على اليسار أدناه لدينا مثال لمسار هاميلتون $(a, b, c, d, e)$, وعلى اليمين لدينا مثال لدورة هاميلتون على نفس المُخطط البياني $(a, b, c, d, e)$:

عندما درسنا مسارات ودوائر أويلر في القسم السابق توصلنا إلى أن هناك شروط بسيطة تحدد ما إذا كان المُخطط البياني يحتوي على مسار و/أو دائرة أويلر. ولم يتم ايجاد ما يعادل هذا في حالة مسارات ودورات هاميلتون. بصورة عامة يُعتبر تحديد ما إذا كان المُخطط البياني يحتوي على مسار و/أو دورة هاميلتون مسألة صعبة جدا.

مسألة التاجر المتجول

احدى المسائل الرياضية التقليدية في مجال نظرية المُخططات البيانية والتي تتعلق تحديدا بالمسارات هي مسألة التاجر المتجول
$)$بالإنجليزية: $(The traveling Salesman Problem (TSP)$.

تتعلق المسألة بزيارة أحد التجار لمجموعة معينة من المدن ويريد معرفة أقصر طريق (قياساً بالمسافة, الزمن او المال) ممكن لإنجاز هذه المهمة, بحيث تكون بداية الرحلة ونهايتها في نفس المدينة.

يمكن تحليل هذه المسألة باستخدام مُخطط بياني، حيث تكون رؤوس هذا المُخطط هي المدن وأضلاعه هي طُرق المواصلات بين المدن. لتحديد المسافة ين رأسين من رؤوس المُخطط البياني يمكن استخدام أوزان أضلاع المُخطط البياني, ويُسمى المُخطط الناتج بالمُخطط الموزون (weighted graph).

فيما يلي لدينا مثال لمُخطط بياني موزون:

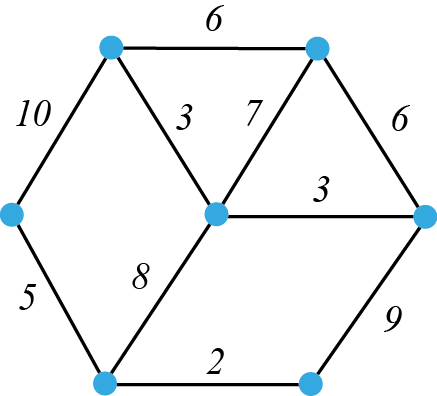
المُخطط البياني الموزون أعلاه يحتوي (على الأقل) على دورة هاميلتون واحدة. هل يمكنك إيجادها؟ ما هو طول دورة هاميلتون (طول الدورة يساوي مجموع أوزان أضلاع الدورة)؟ هل هذه هي أقصر دورة لهاميلتون في المُخطط البياني؟

على الرغم من سهولة تعريف هذه المسألة، إلا أنها غالبًا ما تتطلب العديد من الموارد لحلها عند زيادة حجم مُخططاتها البيانية.

---

ڤيديو الدرس بالسويدية