الحركة، المسارات والدوائر

في القسم السابق تعرفنا على مفهوم المُخطط بالمعنى الذي يحمله في مجال نظرية المُخطط البياني.

في هذا القسم سنبني ما تعلمناه عن المُخططات البيانية من خلال دراسة الحركة والطُرق والمسارات الدائرية في مجال المُخططات البيانية وما هي النتائج التي يمكن استنتاجها من هذا، وبما في ذلك ما يتعلق بما ينطبق على يُسمى بمسارات ودوائر أويلر.

سننهي هذا الباب بدراسة المسارات والحلقات الدائرية, بما في ذلك مسارات وحلقات هاميلتون.

الحركة والمسارات

نفترض أن لدينا مُخطط بياني يمكن توضيحه على النحو التالي:

لنقول أن رؤوس هذا المُخطط البياني تُمثل خمسة مدن وأضلاعه تُمثل ستة طُرق حديدية تربط بين هذه المدن.

إذا كنا على سبيل المثال في المدينة $a$ ونريد الذهاب إلى المدينة $e$ من خلال احدى هذه الطرق الحديدية، فيمكننا القيام بذلك بعدة طُرق. أحد الطُرق الممكنة هو من المدينة $a$ عبر المدينة $d$ إلى المدينة $e$, يمكننا التعبير عن ذلك بتسلسل الرؤوس ($a, d, e$), ولكن يمكننا أيضا اختيار المرور من المدينة $a$ عبر المدينة $d$ والمدينة $c$ إلى المدينة $e$, أي ($a, d, c, e$). كما يمكن أيضا اختيار زيارة نفس المدينة عدة مرات, على سبيل المثال ($a, b, a, d, e$).

نستخدم مصطلح حركة المُشاة أو جولة (بالسويدية vandring) لكل خيار من خيارات طريق الرحلة بحيث تتكون كل جولة من تسلسل معين من رؤوس المُخطط.

$${v}_{1},\,{v}_{2},\,...\,,\,{v}_{n}$$

حيث أن كل رأسين متتاليين متجاورين (أي أن هناك ضلع بينهما).
بالتالي فان السير من خلال تسلسل الرؤوس ($a, d, e$) في المُخطط البياني أعلاه هي عبارة عن خط سير وذلك لأن الرأسين $a$ و $d$ متجاورين وكذلك الرأسين $d$ و$e$ متجاورين.

كما لاحظنا سابقا يمكن أن تحتوي الجولة على نفس الرأس عدة مرات، على سبيل المثال الجولة $\left(a, b, a, d, e\right)$ حيث تمت زيارة الرأس $a$ مرتين. كما يمكن أيضا أن تحتوي الجولة على نفس الضلع أكثر من مرة، كما هو الحال في نفس مثال الجولة $\left(a, b, a, d, e\right)$ حيث تم استخدام الضلع $\left\{a, b\right\}$ مرتين أثناء الرحلة, مرة في الاتجاه من $a$ إلى $b$ ومرة في الاتجاه العكسي من $b$ إلى $a$.

الجولة التي لا يوجد بها ضلع أكثر من مرة تُسمى بالمسار الواحد. لذلك فان الجولة $\left(a, d, e\right)$ هي عبارة عن مسار واحد، ولكن الجولة $\left(a, b, a, d, e\right)$ ليست مسار واحد.

مسار ودائرة أويلر

هنالك نوع خاص من المسارات وغالبا ما يحدث في المسائل الرياضية وهو ما يُسمى بمسار أويلر, على اسم عالم الرياضيات ليونارد أويلر- Leonard Euler. مسار أويلر هو عبارة عن جولة تحتوي على جميع أضلاع المُخطط (مجموعة الأضلاع E) مرة واحدة فقط.

في المثال أعلاه نلاحظ أن الجولة $(d, a, b, c, e, d, c)$ تُمثل مسار أويلر, لأن هذا المسار يمر بكل ضلع من اضلاع المجموعة E:

لقد واجه أويلر هذا النوع من المسارات عندما درس مشكلة جسور/كباري مدينة كونيجسبيرج (التي تُسمى كالينينجراد-Kaliningrad الآن) السبعة المعروفة. يجري نهر بريجيل عبر مدينة كونيجسبيرج (كالينينجراد-Kaliningrad الآن) الى الشاطئ الجنوبي الشرقي لبحر البلطيق والذي بدوره يقسم المدينة إلى منطقتين كبيرتين. بالإضافة إلى ذلك يحتوي النهر على جزيرتين. المناطق الأرضية على جانبي النهر والجزيرتين الموجودتين داخل النهر ترتبط ببعضها البعض بسبعة جسور/كباري كما في الشكل أدناه.

كان أويلر يفكر في مسألة التجول في هذه المدينة، حيث يستطيع المرء أن يتجول فيها بعبور كل جسر من جسور هذه المدينة مره واحدة فقط، بشرط أن يتم الانتقال من منطقة الى أخرى من خلال الجسور فقط بدون أي وسيلة أخرى.

قام أويلر بتحليل هذه المسألة باستخدام المخطط البياني التالي، حيث أن الرؤوس تمثل المناطق الأرضية الأربعة والأضلاع تمثل الجسور السبعة:

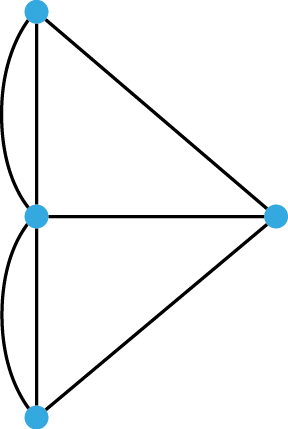
ما توصل إليه أويلر بعد تحليل هذه المسالة هو ايجاد مسار يمر بكل ضلع من أضلاع المخطط البياني مرة واحدة فقط وهو ما سُميَ لاحقاً بمسار/طريق أويلر.

ثم قام بصياغة الشروط اللازمة لكي يحتوي المُخطط البياني على "مسار أويلر" واحد (على الأقل):

لكي يحتوي المُخطط البياني على "مسار أويلر" واحد على الأقل من الضروري أن لا يتجاوز عدد الرؤوس الفردية رأسين فرديين.

يمكن إدراك ضرورة هذا الشرط من خلال المناقشة الغير رسمية التالية:
كل طريقة يصل بها مسار المُخطط البياني أحد الرؤوس ستتطلب أيضاً طريقة لمغادرة هذا الرأس. لذلك يجب أن يحتوي كل رأس من رؤوس المُخطط البياني (الذي يحتوي على مسار أويلر) على عدد زوجي من الأضلاع ما عدا الرؤوس التي يبدأ أو ينتهي بها المسار. بالتالي إذا كان هناك مُخطط بياني يحتوي على مسار أويلر فهذا يعني أن رأسي البداية والنهاية فقط التي يمكن أن تكون فردية.

إذا كان هنالك مُخطط بياني به مسار أويلر واحد (على الأقل) وكانت هنالك رؤوس فردية فهذا يعني أن مسار أويلر سيبدأ وينتهي عند هذه الرؤوس الفردية. وهذا ما يسهل تصنيف مسارات أويلر في المخططات البيانية.

بعد أن تعرفنا على شرط وجود مسار أويلر يمكننا الآن تحديد ما إذا كان المخُطط البياني لمدينة الجسور السبعة (كونيجسبيرغ) يحتوي على مسار أويلر واحد (على الأقل). نلاحظ أن هذا المُخطط البياني يحتوي على رأس من الدرجة 5 وثلاثة رؤوس من الدرجة 3. أي أن جميع رؤوس المُخطط البياني الأربعة هي رؤوس فردية. وبما أن المُخطط البياني يحتوي على أكثر من رأسين فرديين فهذا يعني أن المُخطط البياني لا يحتوي على مسار أويلر ولهذا لا توجد طريقة للسير في هذه المدينة وفقا لمسار أويلر, أي لا يمكن السير في المدينة من خلال كل جسر من جسور المدينة مرة واحدة فقط.

إذا بدأت جولة ما وانتهت عند نفس الرأس وكان مسار هذه الجولة هو مسار أويلر ففي هذه الحالة تُسمى الجولة بدائرة أويلر. هذا التعريف يعني أن جميع دوائر أويلر عبارة عن مسارات أويلر ولكن ليس من الضروري أن يكون العكس صحيح.

بما أن دائرة أولير هي عبارة عن مسار أويلر الذي يبدأ وينتهي في نفس الرأس فيجب أن تكون جميع رؤوس المُخطط البياني زوجية لكي يكون هنالك دائرة أويلر. وهذا ما يعطي الشروط التالية لوجود دوائر أويلر في المُخطط البياني:

يحتوي المُخطط البياني على دائرة أويلر واحدة على الأقل إذا كانت جميع رؤوسه زوجية.

---

حدد ما إذا كانت المُخططات البيانية التالية تحتوي على مسار أويلر و/أو دائرة أويلر.

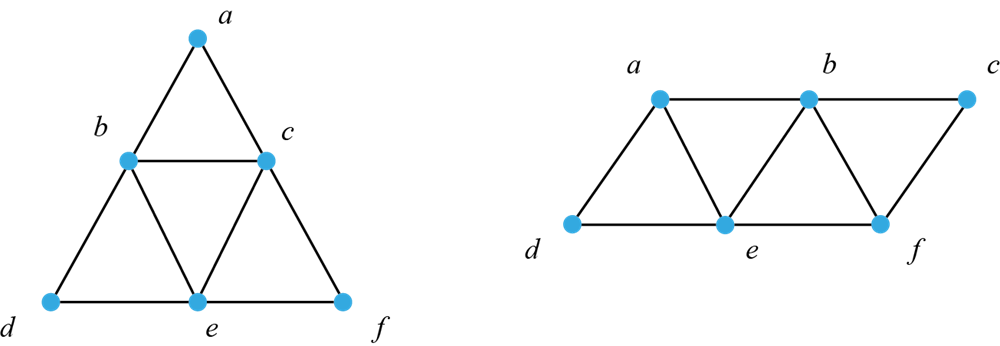
بما أننا نعلم شروط وجود مسارات ودوائر أويلر في المُخططات البيانية سنبدأ بتحديد نوع الرؤوس هل هي فردية أم زوجية.

نلاحظ أن المُخطط البياني على اليسار يحتوي على ثلاثة رؤوس من الدرجة 2 (الرؤوس $a$, $d$ و$f$) وثلاثة رؤوس من الدرجة 4 (الرؤوس $b$, $c$ و $e$). أي أن جميع الرؤوس في المخطط البياني عبارة عن رؤوس زوجية. بالتالي فإن هذه المخطط البياني يحتوي على مسار أويلر واحد (على الأقل) ودائرة أويلر واحدة (على الأقل).

فيما يلي نستعرض دائرة أويلر الممكنة (ومسار أولير) في هذا المخطط البياني وهو $(a, c, f, e, d, b, e, c, b, a)$. كما قد يكون هنالك مسار آخر لأويلر ودائرة أخرى من دوائر أويلر:

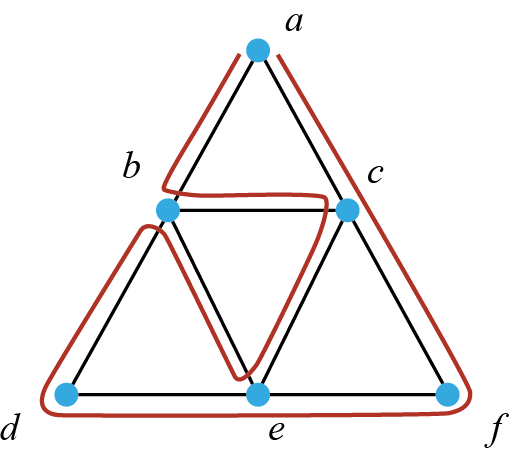
أما المخطط البيان الموجود على اليمين فيحتوي على رأسين من الدرجة 2 (الرأسين $c$ و$d$) ورأسين من الدرجة 3 (الرأسين $a$ و$f$) ورأسين من الدرجة 4 (الرأسين $b$ و$e$). إذن لدينا رأسين فرديين في هذا المخطط (الرؤوس الأربع الأخرى هي رؤوس زوجية). بالتالي فان هذا المخطط البياني يحتوي على مسار أويلر واحد على الأقل. ومع ذلك لا يحتوي هذا المخطط البياني على أي دائرة لأويلر وذلك لأنه ليس جميع رؤوس المخطط البياني زوجية.

بما أن هذا المخطط البياني يحتوي على رأسين فرديين فإن مسار أويلر يجب أن يبدأ عند أحدهما وينتهي عند الرأس الآخر.

فيما يلي نستعرض مسار أويلر الممكن في هذا المخطط البياني وهو $(a, b, c, f, e, d, a, e, b, f)$. كما يمكن وجود مسارات أويلر أخرى غير هذا المسار:

---

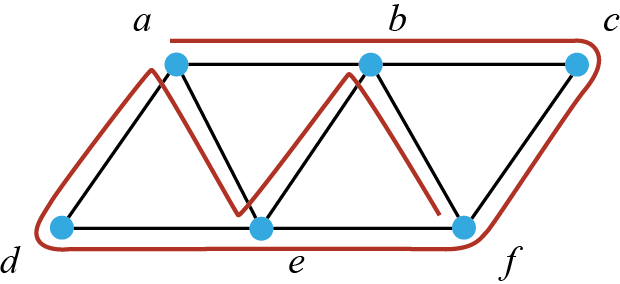
في القسم التالي سنشرح مفاهيم المسارات والدورات بما في ذلك ما يسمى مسارات ودورات هاميلتون التي لا يختلف مفهومها كثيرا عما درسناه في هذا القسم.

---

ڤيديو الدرس بالسويدية