ميل المماس

في القسم السابق تعلمنا كيف يمكننا حساب متوسط الميل بين نقطتين على منحنى باستخدام نسبة التغير.

سيكون من المفيد جدا إذا تمكننا بطريقة ما من تحديد ميل المنحنى عند نقطة ما. النقطة نفسها لا تعطي أي معلومات أكثر من قيمتي \(x\) و \(y\). كيف نعرف ميل المنحنى عند نقطة معينة؟ هل المنحنى عند هذه النقطة مُتجه الى الأعلى أم الى الأسفل أم ربما يكون عند نقطة إنعطاف؟ هذه المعلومات مفيدة جدا في أغلب الأحيان.

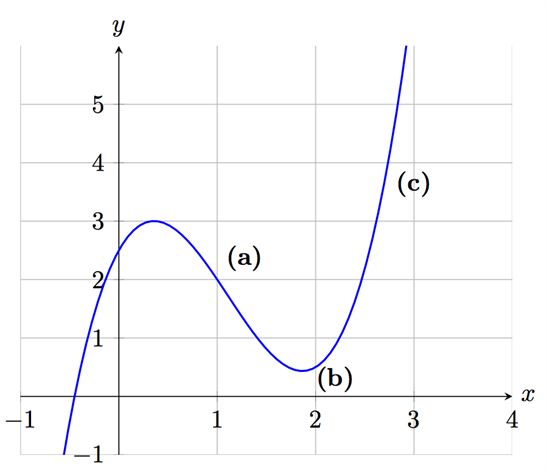
في نظام الإحداثيات أعلاه لدينا رسم بياني للدالة \(f (x)\). نلاحظ أن لدينا نقاط في مواقع مختلفة على المنحنى ووفقا لإختلاف مواقع النقاط يختلف ميل المنحنى من نقطة لأخرى. عند النقطة (a) ينحدر المنحنى الى الأسفل. عند النقطة (b) وبعد نقطة الإنعطاف مباشرة يرتفع المنحنى الى الأعلى. وعند النقطة (c) أيضا يرتفع المنحنى للأعلى وبصورة أكبر من ارتفاعه عند (b).

الآن سنناقش طريقة حساب ميل المنحنى عند نقطة معينة. نبدأ باسترجاع الذاكره حيث نعلم أن أي خط مستقيم له معامل اتجاه (k) يصف ميل الخط. يتم حساب معامل الميل أو قيمة k باستخدام الصيغة التالية:

$$k=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$

الآن لنحسب ميل المنحنى أدناه عند النقطة (b) ونبدأ بتحديد نقطة جديدة بالقرب من النقطة (b). لنسمي هذه النقطة (x):

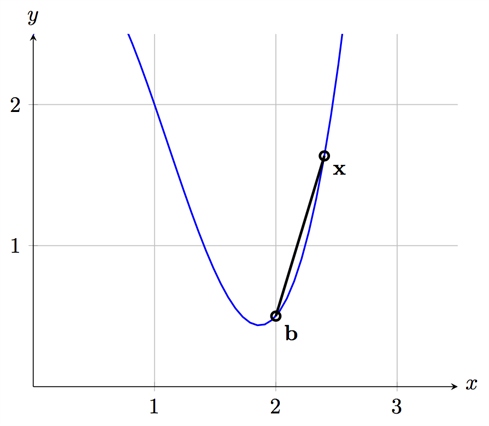
الآن لدينا نقطتين إحداثيتين مختلفتين. إذا وصلنا هاتين النقطتين معا على المنحنى بخط مستقيم (قاطع) فسيكون ميل هذا الخط المستقيم كما يلي:

$$k=\frac{y-y_{b}}{x-x_{b}}$$

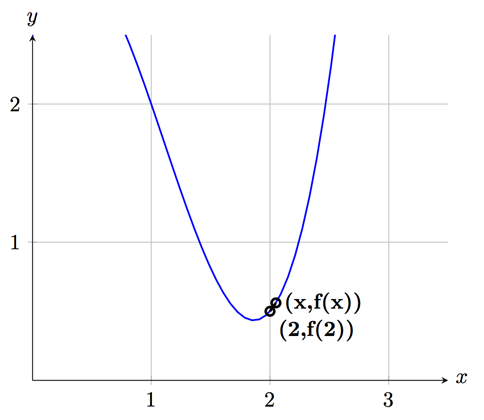
لنحدد الآن قيّم احداثيات كل من \(x\) و \(y\) على الرسم بحيث تكون إحداثيات النقطة (b) هي 2 للإحداثي \(x\) و \(f (2)\) للإحداثي \(y\). أما النقطة (x) فهي نقطة عشوائية ولتكن إحداثياتها \( (x, f(x))\).

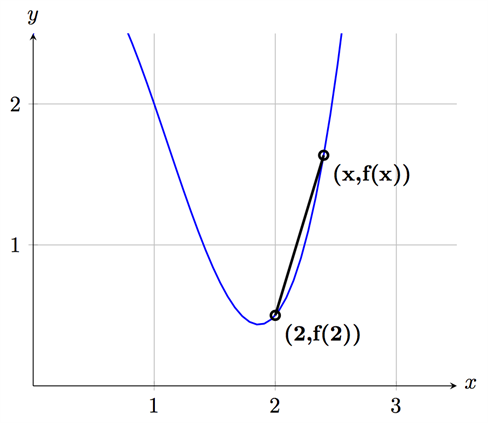
الآن ستكون قيمة k كما يلي:

$$k=\left (\frac{y-y_{b}}{x-x_{b}} \right )=\frac{f(x)-f(2)}{x-2}$$

يُسمى حاصل هذه القسمة بنسبة التغير وهو مشابه للصيغة التي استخدمناها سابقا. الفرق الوحيد هو أننا عوضنا قيّم كل من \(x\) و \(y\) من النقاط الموضحة على الدالة. وتعمل هذه الصيغة تماما كصيغة قيمة الميل k العادية، ولكن بإستخدام تسميات أخرى للإحداثيات.

ماذا يحدث إذا حركنا النقطة (x) على إمتداد المنحنى بحيث تكون قريبة من النقطة (b)؟

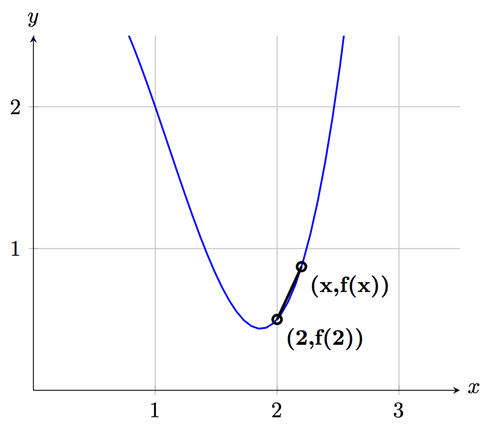
ما يحدث هو أن الخط المستقيم الواصل بين النقطتين سيكون له ميل آخر مختلف (يتغير معامل الميل). قارنه مع الميل في الشكل السابق. إذا واصلنا في تحريك النقطة (x) بحيث تكون أقرب وأقرب من النقطة (b) ستصبح المسافة بين النقطتين قصيرة جدا وقد تصبح شبه معدومة. وكلما حركنا (x) في إتجاه (b) كلما تغيّر الميل حتى يصبح ميل هذا الخط أقرب من الميل عند النقطة (b). يمكننا تقريبا أن نقول أن الميل يمكن قياسه عند النقطة (b) فقط!

اقتراب النقطة (x) من \((x=2)\) بهذه الطريقة يمكن وصفه رياضيا كما يلي:

$$x\to 2$$

وتُقرأ "x تقترب من 2". أخيرا إذا جعلنا النقطة (x) قريبه جدا من النقطة (b) بحيث تكون النقطتين شبه متطابقتين وفي هذه الحالة نكون قد وصلنا إلى ما يُسمى بمنطقة الحدود. فعليه يمكن اعتبار أن ميل الخط بين النقطتين القريبتين جدا من بعضهما البعض له نفس ميل المنحنى عند نقطة معينة وهي النقطة (b) في هذه الحالة.

عندما يكون لدينا خط يلمس المنحنى في نقطة واحدة فقط وله نفس ميل المنحنى عند هذه النقطة، ففي هذه الحالة نقول أن هذا الخط هو عبارة عن مماس لهذا المنحنى عند هذه النقطة.

فيديوهات الدرس

المُشتقات و ميل المماس.

في هذا الفيديو سنستعرض مفهوم المماس.