قواعد حساب التكاملات
في الدورة رياضيات 3 بدأنا شرح مفهوم التكامل ورأينا كيف يمكن حساب الدالة الأولية بناءً على دالة معروفة. كما رأينا أيضًا كيف يمكن استخدام التكاملات لتسهيل حساب المساحات.
في هذا القسم سنوسع معرفتنا بالدوال الأولية كما سنتعلم عدد من قواعد حساب التكاملات المُفيدة.
بعض الدوال الأولية الجديدة
بعد أن درسنا سابقًا كيف يمكن الوصول إلى الدول الأولية لعدد من الدوال المعروفة لقد قدمنا مزيداً من الدوال حيث نريد الآن أن نكون قادرين على حساب دوالها الأولية.
بصورة عامه فإن الدالة \(F(x)\) تُمثل دالة أولية للدالة \(f(x)\) إذا كان
$$F′(x)=f(x)$$
وبما أن الحدود الثابتة عادةً ما تختفي عندما نُفاضل/نشتق الدالة فيمكن كتابة الصورة العامة للدالة الأولية للدالة \(f(x)\) في الصورة
$$F(x) + C$$
حيث \(C\) ثابت.
الدوال الخاصة التي نُريد إيجاد دوالها الأولية الآن هي الدالتان المثلثيتان \(f(x)=sinkx\) و \(f(x)=coskx\) والدالة \(f(x)=\frac{1}{x}\).
لإيجاد الدوال الأولية لهذه الدوال سنستخدم قواعد الاشتقاق التي توصلنا إليها في قسم مشتقات بعض الدوال المُهمة.
فالدالة
$$f(x)=sinkx$$
دالتها الأولية هي
$$F(x)=-\frac{cos\,kx}{k}+C$$
حيث \(k\) و \(C\) ثوابت.
أما الدالة
$$f(x)=cos\,kx$$
فدالتها الأولية هي
$$F(x)=\frac{sin\,kx}{k}+C$$
حيث k و C ثوابت.
وأخيراً الدالة
$$f(x)=\frac{1}{x}$$
دلتها الأولية هي
$$F(x)=ln\,x+C$$
حيث \(C\) ثابت.
دعونا نأخذ مثال
إذا كان لدينا الدالة
$$y(x)=sin\,2x$$
ونريد حساب المساحة بين مُنحنى هذه الدالة ومحور \(x\) في الفترة
$$0\le x\le\frac{\pi}{2}$$
سنبدأ برسم المنحنى لكي نحصل على فكرة عامة عن شكل المنطقة المراد حساب مساحتها.
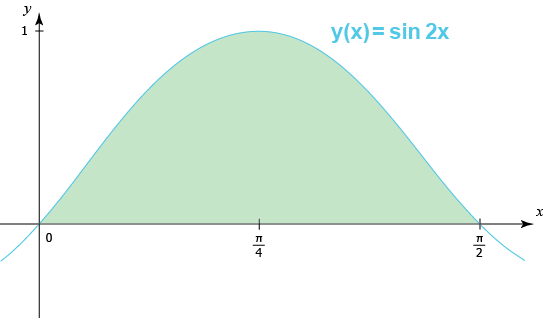
من الدورة رياضيات 3 تعلمنا كيف يمكن حساب المساحة بين المُنحنى \(y(x)\) ومحور \(x\) بإستخدام التكامل التالي
$$A=\int_{a}^{b}y(x)\,dx=Y(b)-Y(a)$$
إذاكانت الدالة \(y(x)\) غير سالبة في الفترة \(a ≤ x ≤ b\).
بتعويض الدالة \(y(x)\) في صيغة المساحة سنحصل على
$$A=\int_{0}^{\frac{\pi}{2}}sin\,2x\,dx$$
يمكن حساب الدالة الأولية للدالة
$$y(x)=sin\,2x$$
بإستخدام الصيغة التي توصلنا اليها أعلاه في هذا القسم:
$$Y(x)=-\frac{cos\,2x}{2}+C$$
الآن يمكننا حساب المساحة كما يلي
$$A=\int_{0}^{\frac{\pi}{2}}sin\,2x\,dx=Y\left (\frac{\pi}{2} \right )-Y(0)=$$
$$=-\frac{cos\,\left (2\cdot \frac{\pi}{2} \right )}{2}+C-\left (-\frac{cos\,(2\cdot 0)}{2}+C \right )=$$
$$=-\frac{cos\,\pi}{2}+C+\frac{cos\,0}{2}-C=$$
$$=-\frac{(-1)}{2}+C+\frac{1}{2}-C=1$$
بالتالي فإن المساحة بين المنحني ومحور \(x\) في الفترة المُحددة هي 1 وحدة مساحة.
قواعد الحساب
هناك عدد من قواعد الحساب التي يمكن إستخدامها في عمليات حساب التكاملات. هذه القواعد يمكن استخدامها على سبيل المثال في تبسيط التكاملات المُعقدة.
فيما يلي سنستعرض هذه القواعد ونأخذ مثال على كل منها.
عملية إخراج الثابت \(k\) خارج عملية التكامل:
$$\int_{a}^{b}k\cdot y(x)\,dx=k\cdot \int_{a}^{b}y(x)\,dx$$
مثال على هذه القاعدة:
$$\int_{a}^{b}2\cdot sin\,x\,dx=2\cdot \int_{a}^{b}sin\,x\,dx$$
عملية تقسيم فترة حدود التكامل الى فترتين:
$$\int_{a}^{c}y(x)\,dx=\int_{a}^{b}y(x)\,dx+\int_{b}^{c}y(x)\,dx$$
مثال على هذه القاعدة:
$$\int_{0}^{\frac{\pi}{2}}sin\,2x\,dx=\int_{0}^{\frac{\pi}{4}}sin\,2x\,dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}sin\,2x\,dx$$
عملية تكامل حدود الدالة بصورة منفصلة بدلاً من تكاملها معاً ومن ثم نضيف هذه التكاملات المنفصلة الى بعضها البعض:
$$\int_{a}^{b}(f(x)+g(x))\,dx=\int_{a}^{b}f(x)\,dx+\int_{a}^{b}g(x)\,dx$$
مثال على هذه القاعدة:
$$\int_{a}^{b}(sin\,x+2x)\,dx=\int_{a}^{b}sin\,x\,dx+\int_{a}^{b}2x\,dx$$
بنفس الطريقة في حالة الطرح, حيث يمكننا تكامل حدود الدالة بصورة منفصلة بدلاً من تكاملها معاً ومن ثم نطرح هذه التكاملات المنفصلة من بعضها البعض:
$$\int_{a}^{b}(f(x)-g(x))\,dx=\int_{a}^{b}f(x)\,dx-\int_{a}^{b}g(x)\,dx$$
مثال على هذه القاعدة:
$$\int_{a}^{b}(sin\,x-2x)\,dx=\int_{a}^{b}sin\,x\,dx-\int_{a}^{b}2x\,dx$$
فيديو الدرس (بالسويدية)
استنتاج الدوال الأولية وتحديد ثوابتها باستخدام القيمة الأولية.
