حساب التكاملات
في القسم السابق تعلمنا كيف يمكن إيجاد الدوال الأولية بإستخدام دالة معلومة. في هذا القسم سنشرح أحد التطبيقات المفيدة للدوال الأولية المتكررة في عدد من السياقات المختلفة. سندرس مفهوم التكاملات ونتعلم كيف يمكننا استخدام التكاملات لحساب المساحات.
عملية حساب تكامل أي دالة هي عبارة عن حساب المساحة بين منحنى الدالة ومحور \(x\).
دعونا نبدأ بمثال
إذا كان لدينا الدالة التالية
$$y(x)=2x+4$$
ونريد معرفة مساحة المنطقة الواقعة بين منحنى هذه الدالة ومحور \(x\) والمحصورة بين الخطين العموديين \(x =0\) و \(x =2\).
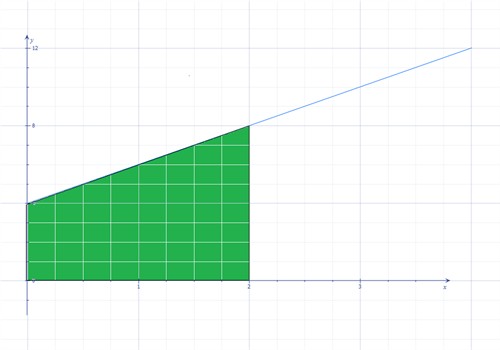
هناك صيغة عامة لحساب هذا النوع من المساحات:
$$\int_{a}^{b}f(x)dx = F(b)-F(a)$$
في بداية الطرف الأيسر لدينا علامة التكامل \(\int \)
الأعداد \(a\) و \(b\) يُمثلان حدود التكامل وهما الحدين الأدنى والاعلى للمساحة المُراد حسابها (وفي هذا المثال، \(a =0\) و \(b =2\)). يمين علامة هذا التكامل المحدود لدينا الدالة التي تُشكل الحد الأعلى لهذه المساحة. وأخيرا في نهاية الطرف الأيسر لدينا \(dx\) والتي تُشير إلى أن حساب المساحة سيتم بالنسبة للتغيّر في إتجاه \(x\).
في الطرف الأيمن لدينا الفرق \(F(b)-F(a)\)
وهو عبارة عن الفرق بين قيمتي الدالة الأولية \(F(b)\) عند الحد الأعلى \((x =b)\) و\(F(a)\) عند الحد الأدنى \((x =a)\).
هناك الكثير من الجديد ولأول مرة نقابله في هذه الصيغة ولذلك من الأسهل المواصلة مع نفس المثال:
بالتالي الدالة المُعطية هي \(y (x) =2x + 4\) ونعلم أن الحد الأدنى هو \(a =0\) وأن الحد الأعلى هو \(b =2\), وهذه المُعطيات سنعوضها في الطرف الأيسر من الصيغة وفي هذه الحالة سنُسمي التكامل الذي يُمثل هذه المساحة بالحرف A كما يلي:
$$A=\int_{0}^{2}(2x+4)dx$$
الطرف الأيمن من الصيغة يُمثل الدالة الأولية \(F\) وهي التي لا نعرفها حتى الآن وفي الخطوة التالية سنحسب الدالة الأولية \(F\) بإستخدام القواعد التي توصلنا إليها في القسم السابق:
$$F(x)=x^{2}+4x+C$$
عند حساب التكامل عادة ما تتم كتابة العملية الحسابية على النحو التالي:
$$\int_{a}^{b}f(x)dx = \left [ F(x) \right ]_a^b$$
وفي هذا المثال ستكون كما يلي
$$\int_{0}^{2}(2x+4)dx = \left [ x^2+4x \right ]_0^2$$
نلاحظ أن في الطرف الأيمن من الصيغة أعلاه تجاهلنا ثابت التكامل \(C\) وذلك لأن هذا الحد سيختفي لأنه موجود في كلٌ من \(F (b)\) و \( F (a)\). ومع ذلك سنأخذ هذا الحد الثابت في هذه العملية الحسابية لكي نرى كيف سيختفي:
$$A=\int_{0}^{2}(2x+4)dx = \left [ x^2+4x \right ]_0^2=$$
$$=(2^{2}+4\cdot 2 + C)-(0^{2}+4\cdot 0 +C)=$$
$$=4+8+C-C=12 \: a.e.$$
إذن المساحة المطلوب حسابها هي 12 وحدة مساحة.
في المثال أعلاه كان لدينا دالة يقع منحناها كليا فوق محور \(x\) وبالتالي فإن المساحة التي نريد حسابها تقع كليا فوق محور \(x\).
كيف ستكون العمليات الحسابية إذا كانت الدالة لها قيّم سالبة في الفترة المُحددة وفي هذه الحالة المساحة المُراد حسابها تقع أسفل محور \(x\)؟ حسنا، إذا إستخدمنا نفس الطريقة أعلاه لحساب عملية التكامل سنحصل على قيمة مساحة سالبة. ولكن قيمة المساحة يجب ألا تكون سالبة، ولهذا يجب علينا تغيير علامة التكامل عندما تكون المساحة المُراد حسابها أسفل محور \(x\).
فيديوهات الدرس
في هذا الفيديو سنشرح التكاملات وكيفية حسابها.
هنا سنشرح معنى مفهوم التكاملات وأهمية حسابها.
كيفية إستخدام الآلات الحاسبة البيانية
هنا تم إستخدام الآلة الحاسبة البيانية Casio FX-CG20.
شاهد نفس التمرين على الآلة الحاسبة البيانية Casio FX-9750GII.
الآلات الحاسبة البيانة من الماركات الأخرى لديها نفس الوظائف تقريباً.
