القيّم الكبرى والصغرى

في القسم السابق درسنا موضوع الزيادة والنقصان في قيّم الدوال وكيفية إرتباط مثل هذه التغيرات بالمشتقة عند نقاط مختلفة على المنحنى.

لنتعمق الآن قليلا ونرجع الى واحدة من الحالات التي درسناها في القسم السابق وهي الحالة التي تكون فيها المشتقة تساوي صفر، وفي مثل هذه الحالات عادة ما يكون المماس عند هذه النقطة أفقي (أي مواز لمحور \(x\)). كما سنرى أيضا متى ستأخذ الدالة أكبر أو أصغر قيمة لها.

نقاط إنعدام المُشتقة

لماذا هذه النقاط التي تكون عندها الُمشتقة تساوي صفرا ذات أهمية بشكل خاص؟ حسنا، عندما تكون المُشتقة صفر وبالتالي فإن المماس سيكون أفقيا موازي لمحور \(x\) فهذا يعني أن النقطة تقع في أعلى المنحنى في القمة (نقطة عظمى)، أو عند أسفل المنحنى في القاع (نقطة صغرى) أو عند نقطة ما تشبه سرج الحصان (نقطة سرجية). النقطة السرجية هي النقطة التي يكون فيها المنحنى متزايد من الجانبين أو متناقص من الجانبين.

بصورة عامة تُسمى النقاط العظمى والصغرى بالنقاط القصوى وذلك لأن الدالة عند النقاط العظمى ستكون قيمتها أكبر من جميع قيّم الدالة الأخرى على إمتداد المنحنى أو على إمتداد فترة محددة على المنحنى وبنفس المفهوم عند النقاط الصغرى ستكون قيمتها أصغر من جميع قيّم الدالة الأخرى على إمتداد المنحنى أوعلى إمتداد فترة محددة على المنحنى وفي كلا الحالتين لدينا قيمة قصوى.

---

في الأشكال أدناه لدينا أمثلة على كل من النقاط العظمى (maximipunkter)، النقاط الصغرى (minimipunkter) والنقاط السرجية (terrasspunkter).

 

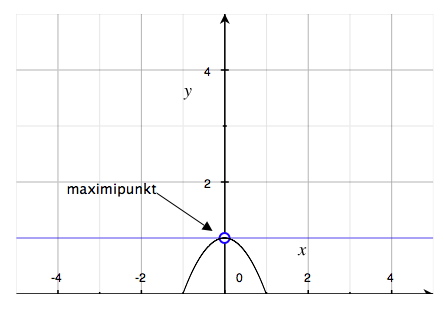
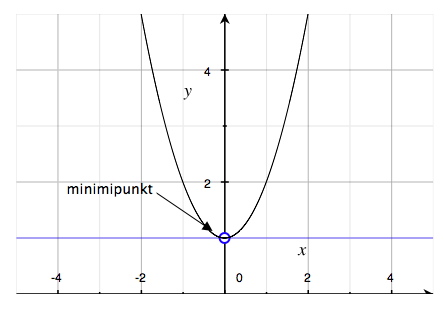
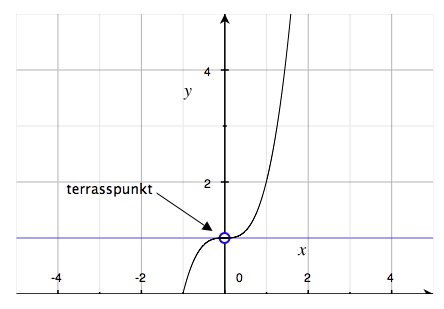
القيّم الكُبرى والصُغرى

تأخذ الدالة قيمتها العُظمى أو الصُغرى عند النقاط القصوى (النقاط العظمى والصغرى) أو عند نقاط نهائية الفترة المُعرفة فيها الدالة (المدى). قد تكون الدالة مُعرفة في فترة معينة كما قد تكون مُعرفة أيضا عند نقطتي بداية ونهاية الفترة.

مثال على دالة ونقاطها القصوى وقيّمها

لندرس الدالة أدناه من خلال قراءة مُنحناها ونتعرف على نقاطها القصوى وقيّم هذه النقاط القصوى وهل هي قيّم عظمى أم صغرى.

$$f(x)=x^{3}+2x^{2}+2$$

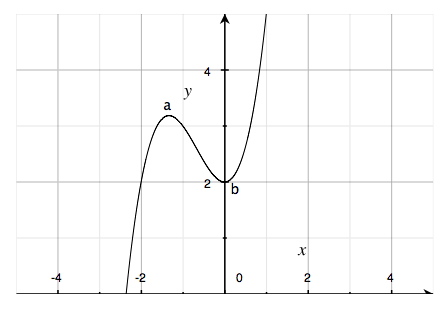
في الرسم أعلاه حددنا نقطتين، نقطة عُظمى محلية (a) ونقطة صُغرى محلية (b). نعلم أن (a) و (b) هما نقاط قصوى محلية لأن المماس أفقي عند هذه النقاط. النقطة (a) تقع في قمة والنقطة (b) تقع في قاع.

يمكننا إيجاد إحداثيات هذه النقاط من خلال إشتقاق الدالة. بما أنها عبارة عن إحداثيات نقاط قصوى فهذا يعني أن المماسات عندها أفقية أي أن ليس لها ميل، ما يعني أن المُشتقة عند هذه النقاط يساوي صفر وبالتالي يمكننا استخدام المعادلة التالية لإيجاد النقاط القُصوى:

$$f'(x)=0$$

لذلك سنحتاج إلى اشتقاق الدالة ومن ثم نساوي تعبير المُشتقة بالصفر ونحل المعادلة التي سنحصل عليها.

سنقوم أولا باشتقاق الدالة بإستخدام قواعد التفاضل التي وصلنا إليها سابقاً:

$$f(x)=x^{3}+2x^{2}+2$$

$$f'(x)=3x^{2}+4x$$

نساوي المُشتقة بالصفر:

$$0=3x^{2}+4x$$

في الختام سنحل هذه المعادلة (في هذه الحالة يمكننا إستخدام طريقة طريقة ناتج الضرب الصفري وهي أسهل طريقة عندما تكون قابلة للتطبيق، ولكن يمكننا أيضا حلها بإستخدام صيغة-pq:

$$0=3x^{2}+4x$$

$$0=x(3x+4)$$

$$\begin{align} x_{1} & =0 \\ x_{2} & =-\frac{4}{3} \end{align}$$

الآن أوجدنا قيّم \(x\) للنقاط القصوى. وبتعويض قيّم \(x\) في الدالة \(f (x)\) يمكننا الحصول على قيّم \(y\) عند هذه النقاط:

$$f(0)=0^{3}+2\cdot 0^{2}+2=2$$

إذن إحداثيات النقطة الصُغرى (b) هي \((0, 2)\).

$$f\left (-\frac{4}{3}\right )=\left ( -\frac{4}{3} \right )^{3}+2\cdot \left ( -\frac{4}{3} \right )^2 +2=$$

$$=-\frac{64}{27}+\frac{32}{9}+2=-\frac{64}{27}+\frac{96}{27}+\frac{54}{27}=$$

$$=\frac{86}{27}$$

عملية حساب قيمة الدالة عند النقطة العُظمى (a) أكثر تعقيدا ولكن أخيرا تم إيجادها وإحداثيات النقطة هي \((-4/3, 86/27)\)، وهي حوالي \((-1,3 ; 3,2)\) تقريبا.

الآن يمكننا أن نقول أن قيّم هذه النقاط عبارة عن نقاط قصوى محلية، أي نقاط قصوى في فترات معينة ولكن لا تُمثل أكبر وأصغر قيّم لكل الدالة. إذا نظرنا مرة أخرى الى شكل منحنى الدالة أعلاه سنلاحظ أن الدالة مستمرة الى الأعلى في الجذء الموجب لمحور \(x\) ومستمرة الى الأسفل في الجذء السالب لمحور \(x\). الدالة مستمرة بهذه الطريقة وليس لها قيمة عُظمى أو قيمة صُغرى.

مثال: دالة مُعرفة في فترة محددة

في هذا المثال سندرس الدالة:

$$f(x)=x^3+3x^2$$

المُعرّفة في الفترة \(- 4 \leq x \leq 2 \).

نريد معرفة أكبر وأصغر قيمة للدالة المُعرّفة في الفترة أعلاه. نبدأ بإيجاد قيّم النقاط القصوى للدالة وذلك عن طريق اشتقاق الدالة ومساواتها بالصفر.

$$f'(x)=3x^2+6x$$

$$\begin{align} 3x^2+6x & =0 \\ x(3x+6) & =0 \end{align}$$

هنا لدينا حاصل ضرب عاملين يساوي صفر، ما يعني أنه يمكننا قراءة العامل الأول مباشرةً \(x_1 = 0\), أما العامل الثاني يمكن إيجاده كما يلي:

$$\begin{align} 3x+6 & =0 \\ 3x & = -6 \\ x_2 & =-2\end{align}$$

إذن أوجدنا قيّم \(x\) للنقاط القصوى. لنوجد الآن قيّم الدالة القصوى (قيّم \(y\)) عند هاتين النقطتين وذلك بتعويض قيّم \(x\) في الدالة:

في حالة \(x_1 = 0\):

$$f(0)=0^3+3\cdot 0^2 = 0$$

وفي حالة \(x_2 = -2\):

$$f(-2)=(-2)^3+3\cdot(-2)^2=-8+12=4$$

فهذا يعني أن لدينا قيّم قصوى للدالة عند تلك النقاط وهي \(y_1 = 0\) (كما كانت مُرشحة أن تكون قيمة صغرى) و \(y_2 = 4\) (كما كانت مُرشحة أن تكون قيمة عظمى).

لكي نتأكد من أن هذه النقاط القصوى هي عبارة عن أكبر وأصغر قيّم للدالة يجب علينا اختبار نقاط نهايتي فترة تعريف الدالة، أي الفترة \(x =-4\) و \(x =2\):

$$f(-4)=(-4)^3+3\cdot (-4)^2=-64+48=-16$$

$$f(2)=2^3+3\cdot 2^2=8+12=20$$

إذن قيمتي الدالة الكُبرى والصُغرى لا تقع عند تلك النقطتين بينما تقعان عند نقاط نهايتي فترة تعريف الدالة. أكبر قيمة للدالة هي \(20\) وأقل قيمة لها هي \(-16\).

فيديوهات الدرس

مفهوم النقاط العُظمى والقيّم العُظمى.

هنا سنشرح كيف يمكننا إيجاد القيّم الكُبرى والصُغرى للدوال في فترة مُعينة.