معادلة القطع المكافئ
هذا القسم يدخل في مقرر رياضيات 2c.
في قسم معادلات الدرجة الثانية تعلمنا أن الرسم البياني لمعادلات الدرجة الثانية عبارة عن قطع مكافئ. في هذه القسم سندرس القطع المكافئ بصورة أوسع ونتعلم كيف يمكن استنباط معادلة القطع المكافئ.
بصورة عامة عادة ما تُكتب دوال الدرجة الثانية كما يلي
$$f(x)=ax^{2}+bx+c$$
حيث أن \(a\), \(b\) و \(c\) أعداد حقيقية و \(a\neq 0\).
أي دالة يمكن كتابتها في هذا الشكل سيكون لها خصائص مُمَيّزة، من خصائص هذا النوع من الدوال أن قيمة الثابت \(a\) ستحدد ما إذا كان الرسم البياني للدالة (القطع المكافئ) سيكون له نقطة صغرى أم نقطة عظمى. قيمة الثابت \(c\) هي التي ستحدد أين يتقاطع القطع المكافئ مع المحور \(y\). بصورة عامة عادة ما تكون القطوع المكافئة متماثلة حول خط تماثل معين؛ خط التماثل هذا يقع في المنتصف بين أصفار الدالة أي بين نقطتي انعدام الدالة \((x_2 \,و\, x_1)\) كما موضح بخط أحمر متقطع في الشكل أدناه.
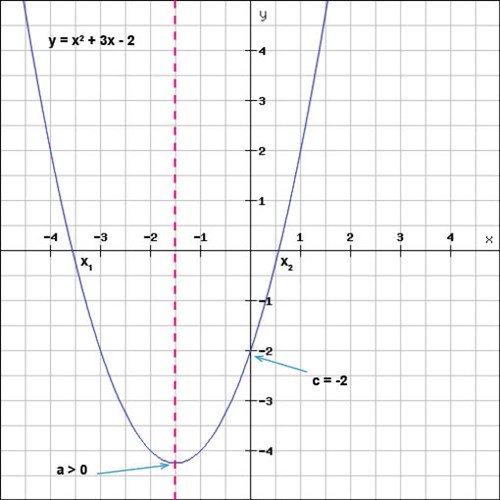
بناء على أن شكل الرسم البياني لدوال الدرجة الثانية عبارة عن قطع مكافئ يمكننا الاستمرار في دراسة القطع المكافئ واستنباط معادلته.
نقطة البؤرة والدليل
يمكن تعريف القطع المكافئ بأن المسافة بين كل نقطة (P) تقع على امتداد القطع المكافئ وبؤرته (Q) تساوي المسافة بين هذه النقطة (P) ودليل القطع المكافئ (S).
نلاحظ هذا المفهوم على نظام الإحداثيات أدناه وفيه لدينا قطع مكافئ له نقطة صغرى عند الأصل:
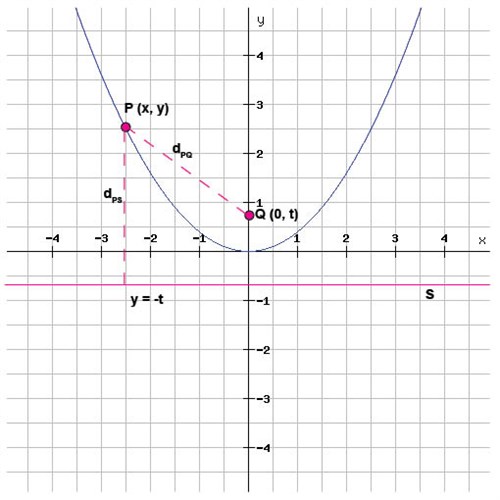
أيضا لكل قطع مكافئ نجد أن النقطة القصوى للقطع المكافئ تقع في منتصف المسافة بين البؤرة والدليل.
مواقع جميع النقاط التي تقع على امتداد القطع المكافئ تعتمد تماما على موقعي نقطة البؤرة والدليل. فإذا علمنا كل من نقطة البؤرة والدليل يمكننا تحديد شكل القطع المكافئ.
معادلة القطع المكافئ
الآن سنقوم باستنباط معادلة القطع المكافئ للحالة الموضحة في الشكل أعلاه، في هذه الحالة إحداثيات نقطة البؤرة Q هي \((0, t)\) ومعادلة خط الدليل هي \(y = -t\), حيث أن \(t\) عدد حقيقي.
باستخدام هذه المُعطيات في صيغة المسافة مع تعريف القطع المكافئ يمكننا استنتاج معادلة القطع المكافئ.
نعلم أن المسافة بين النقطة \(P (x, y)\) ونقطة البؤرة يجب أن تساوي المسافة بين نفس النقطة \(P (x, y)\) والدليل. بالتالي يمكننا كتابة تعبيرين لهاتين المسافتين كل على حدة, هاذين التعبيرين يجب أن يكونا متساويين.
صيغة المسافة هي:
$$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
باستخدام هذه الصيغة يمكننا حساب المسافة بين النقطة \(P (x, y)\) ونقطة البؤرة \(Q (0, t)\) كما يلي:
$$d_{PQ}=\sqrt{(x-0)^2+(y-t)^2}=$$
$$=\sqrt{x^2+(y-t)^2} $$
بنفس الطريقة يمكننا حساب المسافة بين النقطة \(P\) والدليل \(S\) (أقصر مسافة بين P والدليل هي عندما تكون قيمة \(x\) على الدليل هي نفسها عند النقطة \(P\)):
$$d_{PS}=\sqrt{(x-x)^2+(y-(-t))^2}=$$
$$=\sqrt{(y-(-t))^2}=$$
$$=\sqrt{(y+t)^2}=$$
$$=y+t $$
وكما ذكرنا سابقا في تعريف القطع المكافئ نعلم أن المسافة \(d_{PQ}\) تساوي المسافة \(d_{PS}\)، وهذا يعني أنه يمكننا كتابة المعادلة التالية ومن ثم نحاول حلها لإيجاد \(y\):
$$d_{PQ}=d_{PS}$$
$$\sqrt{x^2+(y-t)^2}=y+t$$
بما أن الطرف الأيسر عبارة عن تعبير داخل جذر، سنقوم بتربيع الطرفين:
$$\left (\sqrt{x^2+(y-t)^2} \right )^2=(y+t)^2$$
$$x^2+(y-t)^2=(y+t)^2$$
في هذه الحالة يمكننا إعادة كتابة الطرف الأيسر باستخدام قاعدة التربيع الثانية, وإعادة كتابة الطرف الأيمن باستخدام قاعدة التربيع الأولى. ومن ثم نقوم بتبسيط المعادلة بجمع وطرح الحدود المتشابهة في الطرفين على النحو التالي:
$$ x^2+{\color{Blue} {y^2}}-2ty+{\color{Red}{t^2}}={\color{Blue}{ y^2}}+2ty+{\color{Red} {t^2}}$$
$$x^2-2ty=2ty $$
$$x^2=4ty$$
$$y=\frac{x^2}{4t}$$
هذه المعادلة التي توصلنا إليها أعلاه هي الصيغة العامة لمعادلة القطع المكافئ الذي له نقطة قصوى عند نقطة الأصل وبؤرة عند النقطة \((0, t)\) وله خط دليل \(y = -t\):
$$y=\frac{x^2}{4t}$$
تحديد نقطة البؤرة والدليل
على سبيل المثال إذا كان لدينا دالة من الدرجة الثانية معروفة، كما يلي
$$y(x)=x^2$$
باستخدام الصورة العامة لمعادلة القطع المكافئ يمكننا حساب موقع نقطة البؤرة (قيمة \(t\)، أي قيمة الإحداثي \(y\) لنقطة البؤرة).
بكل بساطة قيمة \(y\) في هذه المعادلة يجب أن تكون نفس قيمة \(y\) في الصورة العامة, بالتالي يمكننا إيجاد قيمة \(t\) بحل المعادلة التالية:
$$\frac{x^2}{4t}=x^2$$
$$\frac{x^2}{4t\cdot x^2}=\frac{x^2}{x^2}$$
$$\frac{1}{4t}=1$$
$$1=4t$$
$$t=\frac{1}{4}=0,25$$
إذن نقطة البؤرة لهذا القطع المكافئ تقع عند النقطة \((0, 0.25)\). وبما أن النقطة القصوى يجب أن تقع في منتصف المسافة بين نقطة البؤرة والدليل، فهذا يعني أن معادلة الدليل هي \(y = -0.25\).
استخدامات القواطع المكافئة المعروفة لدى الناس هي الأطباق الهوائية لاستقبال القنوات الفضائية. هذه الهوائيات مصممة بناء على مفهوم العلاقة بين شكل القطع المكافئ ونقطة البؤرة - وتتركز الأشعة القادمة للطبق الهوائي عند نقطة البؤرة حيث يتم تكبير الإشارة المستقبلة.
فيديو الدرس (باللغة اسويدية)
مراجعة مفهوم القطع المكافئ.
