الأعداد الكسرية

Name: Tal i bråkform
Uploaded: 2011-02-08
Description: وسائل مساعدة

عندما يُكتب عدد ما في صورة كسرية سيكون في صورة حاصل قسمة لم يتم حسابها بعد. وفيما يلي مثال على عدد كسري:

$$\frac{3}{4}$$

العدد الكسري يحتوي على بسط ومقام. البسط هو العدد الذي يقع فوق شريط الكسر (في المثال أعلاه البسط هو 3)، بينما المقام هو العدد الذي يقع تحت شريط الكسر (في المثال أعلاه المقام هو 4).

يمكننا حساب الكسر الاعتيادي في المثال أعلاه بقسمة البسط (3) علـى المقام (4) والحصول على الناتج 0,75. في بعض الأحيان من الأفضل حساب التعبيرات الكسرية بهذه الطريقة، ولكن قد يكون في أحيان أخرى من الأفضل تركه في الصورة الكسرية.

مثال على مثل هذه الحالة إذا كان لدينا التعبير

$$\frac{2}{7}+\frac{3}{7}$$

إذا قمنا بحساب كل حد من هذه الحدود بصورة منفصلة سنحصل على أعداد بها منازل عشرية عديدة، كما سيكون مجموعهما. وإذا كتبنا هذا التعبير في صورة كسر عشري سيصبح تعبير آخر له نفس قيمة التعبير الأصلي بالتقريب.

ومع ذلك إذا لم نقم بحساب حاصل قسمة هاذين الحدين وبدلا من ذلك قمنا بتطبيق القواعد الحسابية التي سنبدأ دراستها في هذا القسم ونواصل دراستها الأقسام التالية، عندها يمكننا الحصول على تعبير له نفس قيمة التعبير الأصلي بالضبط، وإضافة الى ذلك سيكون في صورة أبسط. أيضا قد يكون من السهل وصف علاقة أو حالة معينة بترك العدد كما هو في الصورة الكسرية.

في المثال التالي سنرى كيف يمكننا التعبير‏عن علاقة أو حالة معينة باستخدام الكسور الاعتيادية:

فصل دراسي به 12 طالب، ثلاثة منهم يستخدمون نظّارة‏. ما هي نسبة الطلاب الذين يستخدمون النظّارة‏؟

نسبة الطلاب الذين يرتدون نظّارة تُعتبر جزء من الكل (ثلاثة من 12 طالب)، وبمعنى آخر هي عدد الطلاب الذين يرتدون نظّارة مقسوما على عدد الطلاب الكلي في الفصل:

$$\frac{3}{12}$$

إذن ثلاث طلاب من اثني عشر طالبا (ثلاث علـى اثني عشر من إجمالي الطلاب) يرتدون نظارة.

تقسيم الكعكة

تخيل أن لدينا كعكة. فكلما زاد تقسيم الكعكة إلى قطع أكثر كلما صغر حجم القطعة الواحدة. فإذا قمنا بتقسيم الكعكة إلى ثلاث قطع متساوية وأكلنا إحدى هذه القطع فإننا أخذنا $\frac {1} {3}$ الكعكة. وإذا قمنا بدلا من ذلك بتقسيم الكعكة إلى قطعتين متساويتين فقط وأكلنا إحدى هاتين القطعتين بالتالي أكلنا $\frac {1} {2}$ الكعكة، وفي هذه الحالة نكون حصلنا على قطعة أكبر مما إذا قسمناها إلى ثلاث قطع:

$\frac{1}{3}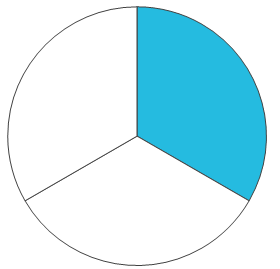$ tal_i_brakform_03 $\frac{1}{2}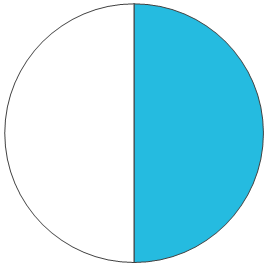$ tal_i_brakform_04

إذا قمت بتقسيم الكعكة إلى 12 قطعة متساوية وأكلت ثلاث قطع منها، فكأنك أخذت $\frac{3}{12}$ من الكعكة. وفي الحقيقة إذا أكلت $\frac{3}{12}$ من الكعكة كأنك قسمت الكعكة الى أربع قطع وأكلت $\frac{1}{4 }$ الكعكة, أي أنك أكلت نفس المقدار من الكعكة في كلا الحالتين, كما سنلاحظ في الصور التالية. الفرق الوحيد هو أنك أكلت في الحالة الأولى ثلاث قطع صغيرة بينما أكلت في الحالة الثانية قطعة واحدة تساوي ثلاثة أضعاف قطعة الحالة الأولى.

$\frac{3}{12}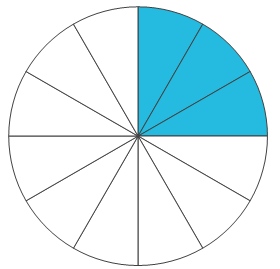$ tal_i_brakform_05 $\frac{1}{4}$ tal_i_brakform_06

يمكن وصف هذا التشابه كما يلي:

$$\frac{3}{12}=\frac{1}{4}$$

عملية الكسور هي نفس طريقة تقسيم الكعكة (يمكنك التفكير في الكسور كالكعكة إذا أردت). فكلما زاد التقسيم الى عدد قطع أكثر كلما كانت القطعة (الجزء) أصغر - وكلما كان الجزء من الكل أصغر كلما كان المقام أكبر في التعبير الكسري. لذلك

$$\frac{1}{3}$$

أقل من

$$\frac{1}{2}$$

في الحالة الأولى (حالة الثُلث) قسمنا الكل إلى ثلاثة أجزاء متساوية، بالتالي سيكون كل جزء منها أصغر مما أذا قسمناه إلى جزأين متساويين.